题目内容
13. 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$如图所示.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$如图所示.(Ⅰ)作出向量2$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$(请保留作图痕迹);
(Ⅱ)若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°,求$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角的余弦值.
分析 (I)运用向量的加减运算的几何性质求解绘画,
(II)根据向量的运算得出$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{1+4+2\sqrt{2}}$=$\sqrt{5+2\sqrt{2}}$,$\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}$=$\sqrt{1+4-2\sqrt{2}}$$\sqrt{5-2\sqrt{2}}$
利用夹角得出cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{a}-\overrightarrow{b}|}$,求解即可.
解答 解:(I)先做出2$\overrightarrow{a}$,再作出$\frac{1}{2}\overrightarrow{b}$,最后运用向量的减法得出2$\overrightarrow{a}$$-\frac{1}{2}\overrightarrow{b}$,如图表示红色的向量,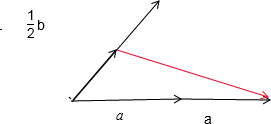
(II)设$\overrightarrow{a}$$+\overrightarrow{b}$,$\overrightarrow{a}$$-\overrightarrow{b}$的夹角θ,
∵|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°
∴$\overrightarrow{a}$$•\overrightarrow{b}$=1×2×cos45°=$\sqrt{2}$,
∴$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{1+4+2\sqrt{2}}$=$\sqrt{5+2\sqrt{2}}$,
$\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}$=$\sqrt{1+4-2\sqrt{2}}$$\sqrt{5-2\sqrt{2}}$,($\overrightarrow{a}+\overrightarrow{b}$)$•(\overrightarrow{a}-\overrightarrow{b})$=1-4=-3,
cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|•|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{-3}{\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}}$=$\frac{-3}{\sqrt{5+2\sqrt{2}}×\sqrt{5-2\sqrt{2}}}$=$\frac{-3}{\sqrt{17}}$=$-\frac{3\sqrt{17}}{17}$.
点评 本题考察了平面向量的加减运算,数量积,向量的模的计算,属于向量的典型的题目,难度不大,计算准确即可.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | y=ln(x+1) | B. | y=xsinx | C. | y=x-x3 | D. | y=3x+sinx |
| A. | [-3,3] | B. | [-1,3] | C. | {-3,3} | D. | [-1,-3,3] |
| A. | x=-π | B. | x=$\frac{π}{4}$ | C. | x=π | D. | x=$\frac{3π}{2}$ |
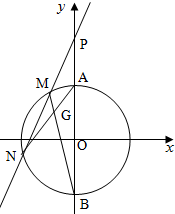 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.