题目内容
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,上、下顶点分别是
,上、下顶点分别是 ![]() ,点
,点 ![]() 是
是 ![]() 的中点,若
的中点,若 ![]() ,且
,且 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 交于不同的两点
交于不同的两点 ![]() ,求
,求 ![]() 的面积的最大值.
的面积的最大值.
【答案】
(1)
由题意可得 ![]() ,
, ![]() ①,由
①,由 ![]() ,可得
,可得 ![]() ,即有
,即有 ![]() ②,由①②解得c=1,b=
②,由①②解得c=1,b= ![]() ,
, ![]() ,故椭圆C的标准方程为
,故椭圆C的标准方程为 ![]() .
.
(2)
设 ![]() ,
, ![]() .
.
由题意知,直线l的斜率不为零,可设直线l 的方程为x=my+1,
由 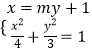 得
得 ![]() ,∴,
,∴, ![]() ,
, ![]() .
.
因为直线l与椭圆C交于不同的两点,
所以△>0,即 ![]() ,则
,则 ![]()
令 ![]() 则t≥1,则
则t≥1,则 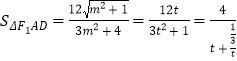 ,令
,令 ![]() ,由函数的性质可知,函数
,由函数的性质可知,函数 ![]() 在
在 ![]() 上是单调递增函数,即当t≥1时,
上是单调递增函数,即当t≥1时, ![]() 在
在 ![]() 上单调递增,因此有
上单调递增,因此有 ![]() ,所以
,所以 ![]() 即当t=1,即m=0时,
即当t=1,即m=0时, ![]() 最大,最大值为3.
最大,最大值为3.
【解析】本题考查椭圆的方程,直线与椭圆的位置关系,构建代数方法解决几何问题等基础知识,意在考查转化与化归能力,综合分析问题、解决问题的能力,推理能力和运算能力.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目