题目内容
已知两条不同直线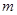 、
、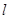 ,两个不同平面
,两个不同平面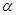 、
、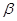 ,给出下列命题:
,给出下列命题:
①若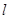 垂直于
垂直于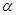 内的两条相交直线,则
内的两条相交直线,则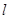 ⊥
⊥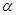 ;
;
②若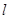 ∥
∥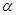 ,则
,则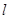 平行于
平行于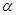 内的所有直线;
内的所有直线;
③若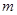
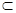
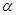 ,
,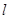
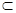
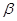 且
且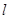 ⊥
⊥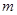 ,则
,则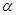 ⊥
⊥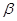 ;
;
④若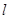
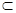
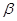 ,
,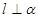 ,则
,则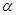 ⊥
⊥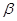 ;
;
⑤若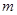
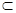
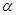 ,
,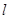
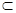
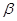 且
且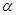 ∥
∥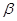 ,则
,则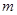 ∥
∥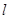 ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
【答案】
①④.
【解析】
试题分析:①由直线与平面垂直的判定定理可知此命题正确;
②错,直线l与平面内的直线也可能异面.
③一个平面内的一条直线垂直另一个平面的一条直线,两个平面不一定垂直,故错.
④若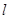
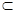
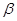 ,
,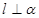 ,则
,则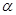 ⊥
⊥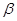 ,符合面面垂直的判定定理,故正确;
,符合面面垂直的判定定理,故正确;
⑤m与l也可能异面,故错.
所以正确命题的序号为①④.
考点:线面垂直,面面垂直的判定与性质,两条直线的位置关系.
点评:掌握线面垂直,面面垂直的判定与性质是判定线面,面面垂直关系的前提,在研究空间两条直线的位置关系时,要从相交,平行,异面三种情况来考虑.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目