题目内容
过点P(1,4)引一条直线,使它在两条坐标轴上的截距为正值,且它们的和最小,求这条直线的方程.
2x+y-6=0
(解法1)设所求的直线方程为y-4=k(x-1).显见,上述直线在x轴、y轴上的截距分别为1-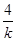 、4-k.由于1-
、4-k.由于1-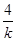 >0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=
>0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=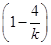 +(4-k)=5+(-k)+
+(4-k)=5+(-k)+ ≥5+4=9,当且仅当-k=-
≥5+4=9,当且仅当-k=-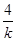 ,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.
,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.
(解法2)设所求的直线方程为 =1(a>0,b>0).
=1(a>0,b>0).
据题设有 =1,① 令S=a+b.②
=1,① 令S=a+b.②
①×②,有S=(a+b) =5+
=5+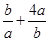 ≥5+4=9.当且仅当
≥5+4=9.当且仅当 时,即2a=b,且
时,即2a=b,且 =1,也即a=3,b=6时,取等号.
=1,也即a=3,b=6时,取等号.
故所求的直线方程为 =1,即2x+y-6=0.
=1,即2x+y-6=0.
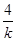 、4-k.由于1-
、4-k.由于1-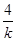 >0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=
>0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=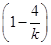 +(4-k)=5+(-k)+
+(4-k)=5+(-k)+ ≥5+4=9,当且仅当-k=-
≥5+4=9,当且仅当-k=-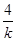 ,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.
,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.(解法2)设所求的直线方程为
 =1(a>0,b>0).
=1(a>0,b>0).据题设有
 =1,① 令S=a+b.②
=1,① 令S=a+b.②①×②,有S=(a+b)
 =5+
=5+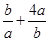 ≥5+4=9.当且仅当
≥5+4=9.当且仅当 时,即2a=b,且
时,即2a=b,且 =1,也即a=3,b=6时,取等号.
=1,也即a=3,b=6时,取等号.故所求的直线方程为
 =1,即2x+y-6=0.
=1,即2x+y-6=0.
练习册系列答案
相关题目
 中,若圆
中,若圆 上存在
上存在 ,
, 两点,且弦
两点,且弦 的中点为
的中点为 ,则直线
,则直线 的方程为 .
的方程为 . 



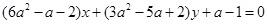 表示平行于x轴的直线,则
表示平行于x轴的直线,则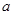 的值是( )
的值是( )