题目内容
已知斜率为1的直线l与双曲线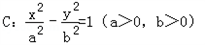 相交于B、D两点,且BD的中点为M(1,3).
相交于B、D两点,且BD的中点为M(1,3).
(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线g:x﹣y+9=0上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程.
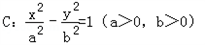 相交于B、D两点,且BD的中点为M(1,3).
相交于B、D两点,且BD的中点为M(1,3).(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线g:x﹣y+9=0上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程.
解:(1)由题设知:l的方程为y=x+2,代入双曲线 ,
,
并化简得:(b2﹣a2)x2﹣4a2x﹣4a2﹣a2b2=0,(*)
设B(x1,y1),D(x2,y2),
则 ,
, ,
,
由M(1,3)为BD的中点,知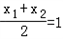 ,
,
故 ,即b2=3a2.故c=2a,∴e=2.
,即b2=3a2.故c=2a,∴e=2.
(2)双曲线的左、右焦点为F1(﹣3,0),F2(3,0),
点F1关于直线g:x﹣y+9=0 ①的对称点F的坐标为(﹣9,6),
直线FF2的方程为x+2y﹣3=0, ②
解方程组①②得:交点M(﹣5,4),
此时|MF1|+|MF2|最小,
所求椭圆的长轴 ,
,
∴a=3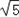 ,
,
∵c=3,
∴b2=36,
故所求椭圆的方程为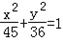 .
.
 ,
,并化简得:(b2﹣a2)x2﹣4a2x﹣4a2﹣a2b2=0,(*)
设B(x1,y1),D(x2,y2),
则
 ,
, ,
,由M(1,3)为BD的中点,知
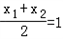 ,
,故
 ,即b2=3a2.故c=2a,∴e=2.
,即b2=3a2.故c=2a,∴e=2.(2)双曲线的左、右焦点为F1(﹣3,0),F2(3,0),
点F1关于直线g:x﹣y+9=0 ①的对称点F的坐标为(﹣9,6),
直线FF2的方程为x+2y﹣3=0, ②
解方程组①②得:交点M(﹣5,4),
此时|MF1|+|MF2|最小,
所求椭圆的长轴
 ,
,∴a=3
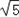 ,
,∵c=3,
∴b2=36,
故所求椭圆的方程为
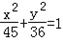 .
.
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 已知斜率为1的直线l与双曲线C:
已知斜率为1的直线l与双曲线C: