题目内容
已知f（x）的图象是连续不断的，有如下的x与f（x）的对应值表：
则函数f（x）存在零点的区间是
则函数f（x）存在零点的区间是
（2，3）（4，5）
（2，3）（4，5）
．分析：利用根的存在性定理：f（x）的图象在区间[a，b]上连续，且f（a）f（b）＜0则f（x）在（a，b）上有根，结合题中的表求出函数f（x）存在零点的区间．
解答：解：据根的存在性定理知：
f（x）的图象在区间[a，b]上连续，且f（a）f（b）＜0则f（x）在（a，b）上有根
有表知函数f（x）存在零点的区间是（2，3） （4，5）
故答案为（2，3） （4，5）．
f（x）的图象在区间[a，b]上连续，且f（a）f（b）＜0则f（x）在（a，b）上有根
有表知函数f（x）存在零点的区间是（2，3） （4，5）
故答案为（2，3） （4，5）．
点评：本题考查利用根的存在性定理判断函数的零点所在的区间．
练习册系列答案
教材全解字词句篇系列答案
相关题目
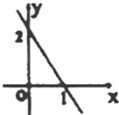已知函数y=f（x）的定义域为R，且满足f（1）=2，其导函数为f′（x）的图象如图，则函数y=f（x）的图象是（ ）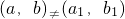
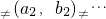
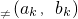，若f（a）＜0，f（b）＞0，则f（bk）的符号为