题目内容
1.在△ABC中,a,b,c分别为内角A,B,C所对的边,且A=$\frac{π}{6}$.现给出三个条件:①a=2; ②B=45°;③c=$\sqrt{3}$b.试从中选出两个可以确定△ABC的条件,并以此为依据求△ABC的面积.(只需写出一个选定方案即可)你选择的条件是①②;(用序号填写)由此得到的△ABC的面积为$\sqrt{3}+1$.
分析 根据条件和正弦、余弦定理选择方案,分别利用正弦、余弦定理求出三角形的边或角,代入三角形的面积公式求出△ABC的面积.
解答 解:(1)①a=2; ②B=45°可以确定三角形,
由正弦定理得:$\frac{a}{sinA}=\frac{b}{sinB}$,则b=$\frac{asinB}{sinA}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=2$\sqrt{2}$,
又C=180°-A-B=105°,则sinC=sin(45°+60°)=$\frac{\sqrt{2}}{2}(\frac{1}{2}+\frac{\sqrt{3}}{2})$=$\frac{\sqrt{2}+\sqrt{6}}{4}$,
所以△ABC的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}×2×2\sqrt{2}×\frac{\sqrt{2}+\sqrt{6}}{4}$=$\sqrt{3}+1$;
(2)①a=2,③c=$\sqrt{3}$b可以确定三角形,
由余弦定理得:a2=b2+c2-2bccosA,
则4=${b}^{2}+{3b}^{2}-2\sqrt{3}{b}^{2}×\frac{\sqrt{3}}{2}$,解得b=2,
则c=2$\sqrt{3}$,即△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×2×2\sqrt{3}×\frac{1}{2}$=$\sqrt{3}$,
故答案为:①②或①③;$\sqrt{3}+1$或$\sqrt{3}$.
点评 本题考查了正弦、余弦定理,以及三角形面积公式的应用,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
16.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个顶点到一条渐近线的距离为$\frac{a}{2}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
13.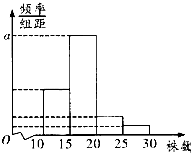 某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
(1)求出表中M,p及图中a的值;
(2)单位决定对参加植树的职工进行表彰,对植树株数在[25,30)区间的职工发放价值800元的奖品,对植树株数在[20,25)区间的职工发放价值600元的奖品,对植树株数在[15,20)区间的职工发放价值400元的奖品,对植树株数在[10,15)区间的职工发放价值200元的奖品,在所取样本中,任意取出2人,并设X为此二人所获得奖品价值之差的绝对值,求X的分布列与数学期望E(X).
 某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:(1)求出表中M,p及图中a的值;
(2)单位决定对参加植树的职工进行表彰,对植树株数在[25,30)区间的职工发放价值800元的奖品,对植树株数在[20,25)区间的职工发放价值600元的奖品,对植树株数在[15,20)区间的职工发放价值400元的奖品,对植树株数在[10,15)区间的职工发放价值200元的奖品,在所取样本中,任意取出2人,并设X为此二人所获得奖品价值之差的绝对值,求X的分布列与数学期望E(X).
| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30) | 1 | 0.05 |
| 合计 | M | 1 |