题目内容
已知函数![]() 图像上的点
图像上的点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若函数![]() 在
在![]() 时有极值,求
时有极值,求![]() 的表达式
的表达式
(2)函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围
的取值范围
(1)![]() (2)实数
(2)实数![]() 的取值范围为
的取值范围为![]()
解析:
已知![]() 在
在![]() 处有极值,等价于
处有极值,等价于![]() 。
。
求函数的解析式一般用待定系法法,求参数的取值范围一般需建立关于参数的不等式(组)![]() , -----------------2分
, -----------------2分
因为函数![]() 在
在![]() 处的切线斜率为-3,
处的切线斜率为-3,
所以![]() ,即
,即![]() ,------------------------3分
,------------------------3分
又![]() 得
得![]() 。------------------------4分
。------------------------4分
(1)函数![]() 在
在![]() 时有极值,所以
时有极值,所以![]() ,-------5分
,-------5分
解得![]() ,------------------------------------------7分
,------------------------------------------7分
所以![]() .------------------------------------8分
.------------------------------------8分
(2)因为函数![]() 在区间
在区间![]() 上单调递增,所以导函数
上单调递增,所以导函数![]()
在区间![]() 上的值恒大于或等于零,--------------------------------10分
上的值恒大于或等于零,--------------------------------10分
则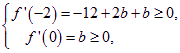 得
得![]() ,所以实数
,所以实数![]() 的取值范围为
的取值范围为![]() ----14分
----14分

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 图像上的点
图像上的点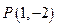 处的切线方程为
处的切线方程为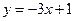 .
.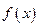 在
在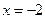 时有极值,求
时有极值,求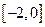 上单调递增,求实数
上单调递增,求实数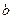 的取值范围
的取值范围 图像上的点
图像上的点 处的切线方程为
处的切线方程为 .
. 在
在 时有极值,求
时有极值,求 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. 图像上的点
图像上的点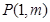 处的切线方程为
处的切线方程为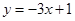 .[来
.[来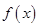 在
在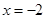 时有极值,求
时有极值,求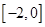 上单调递增,求实数
上单调递增,求实数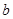 的取值范围。
的取值范围。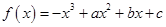 图像上的点
图像上的点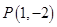 处的切线方程为
处的切线方程为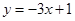 .
.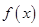 在
在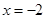 时有极值,求
时有极值,求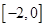 上单调递增,求实数
上单调递增,求实数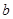 的取值范围
的取值范围