题目内容
已知函数 图像上的点
图像上的点 处的切线方程为
处的切线方程为 .
.
(1)若函数 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
【答案】
(1)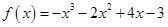 。 (2)
。 (2)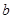 的取值范围为
的取值范围为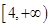 .
.
【解析】本试题主要是考查了导数在研究哈数中的运用。利用函数的导数求解极值,和函数的单调性求解参数的取值范围的综合运用。
(1)函数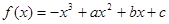 图像上的点
图像上的点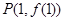 处的切线方程为
处的切线方程为 .可知在x=1处导数为零,同时函数
.可知在x=1处导数为零,同时函数 在
在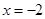 时有极值,所以
时有极值,所以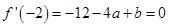 ,那么可以解得a,b,c的值。
,那么可以解得a,b,c的值。
(2)因为函数 在区间
在区间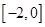 上单调递增,所以导函数
上单调递增,所以导函数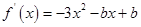 在区间
在区间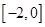 上的值恒大于或等于零,那么利用分离参数的思想得到取值范围。或者借助于函数图像得到。
上的值恒大于或等于零,那么利用分离参数的思想得到取值范围。或者借助于函数图像得到。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 图像上的点
图像上的点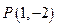 处的切线方程为
处的切线方程为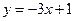 .
.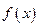 在
在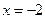 时有极值,求
时有极值,求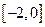 上单调递增,求实数
上单调递增,求实数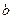 的取值范围
的取值范围 图像上的点
图像上的点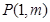 处的切线方程为
处的切线方程为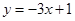 .[来
.[来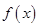 在
在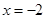 时有极值,求
时有极值,求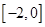 上单调递增,求实数
上单调递增,求实数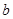 的取值范围。
的取值范围。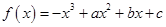 图像上的点
图像上的点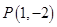 处的切线方程为
处的切线方程为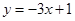 .
.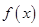 在
在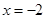 时有极值,求
时有极值,求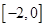 上单调递增,求实数
上单调递增,求实数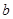 的取值范围
的取值范围