题目内容
已知两个单位向量
，
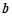的夹角为60°，
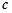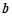= t+（1 - t）,若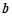·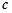= 0，则实数t的值为 ．
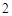
解析试题分析：由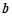·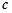= 0得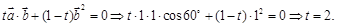
向量数量积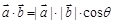
是将两个向量转化为一个实数的过程.
考点：向量数量积.
练习册系列答案
智能训练练测考系列答案
相关题目
题目内容
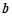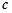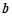已知两个单位向量，的夹角为60°，= t+（1 - t）,若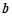·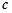= 0，则实数t的值为 ．
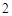
解析试题分析：由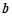·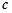= 0得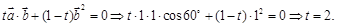
向量数量积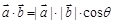是将两个向量转化为一个实数的过程.
考点：向量数量积.
智能训练练测考系列答案
在向量
方向上的投影为 ．
是夹角为
的单位向量，且
，
，则
.
的最小值是 ________________； 
，
，
，则
与
夹角的正弦值为_____.
·
的最小值为________．
与
的夹角为120°，且|
＝λ
，则实数λ的值为________．
·
的最大值是________．