题目内容
已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c,设O为S在底面ABC上的射影.求证:(1)O为△ABC的垂心;
(2)O在△ABC内;
(3)设SO=h,则
 +
+ +
+ =
= .
.
【答案】分析:(1)只需证明O在△ABC的三条高线上,即可证明O为△ABC的垂心;
(2)只需证明△ABC是锐角三角形,即可证明O在△ABC内;
(3)设SO=h,利用等面积法:SB•SC=BC•SD、SA•SD=AD•SO,推得关系化简为 +
+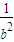 +
+ =
= .
.
解答: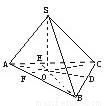 证明:(1)∵SA⊥SB,SA⊥SC,
证明:(1)∵SA⊥SB,SA⊥SC,
∴SA⊥平面SBC,BC?平面SBC.∴SA⊥BC.
而AD是SA在平面ABC上的射影,∴AD⊥BC.
同理可证AB⊥CF,AC⊥BE,故O为△ABC的垂心.
(2)证明△ABC为锐角三角形即可.不妨设a≥b≥c,
则底面三角形ABC中,AB= 为最大,从而∠ACB为最大角.
为最大,从而∠ACB为最大角.
用余弦定理求得cos∠ACB=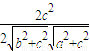 >0,
>0,
∴∠ACB为锐角,△ABC为锐角三角形.故O在△ABC内.
(3)SB•SC=BC•SD,
故SD= ,
, =
=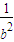 +
+ ,又SA•SD=AD•SO,
,又SA•SD=AD•SO,
∴ =
= =
= =
= +
+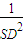 =
=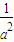 +
+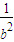 +
+ =
=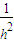 .
.
点评:本题考查棱锥的结构特征,余弦定理,考查空间想象能力,逻辑思维能力,是中档题.
(2)只需证明△ABC是锐角三角形,即可证明O在△ABC内;
(3)设SO=h,利用等面积法:SB•SC=BC•SD、SA•SD=AD•SO,推得关系化简为
 +
+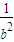 +
+ =
= .
.解答:
 证明:(1)∵SA⊥SB,SA⊥SC,
证明:(1)∵SA⊥SB,SA⊥SC,∴SA⊥平面SBC,BC?平面SBC.∴SA⊥BC.
而AD是SA在平面ABC上的射影,∴AD⊥BC.
同理可证AB⊥CF,AC⊥BE,故O为△ABC的垂心.
(2)证明△ABC为锐角三角形即可.不妨设a≥b≥c,
则底面三角形ABC中,AB=
 为最大,从而∠ACB为最大角.
为最大,从而∠ACB为最大角.用余弦定理求得cos∠ACB=
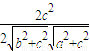 >0,
>0,∴∠ACB为锐角,△ABC为锐角三角形.故O在△ABC内.
(3)SB•SC=BC•SD,
故SD=
 ,
, =
=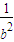 +
+ ,又SA•SD=AD•SO,
,又SA•SD=AD•SO,∴
 =
= =
= =
= +
+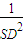 =
=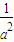 +
+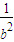 +
+ =
=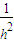 .
.点评:本题考查棱锥的结构特征,余弦定理,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目