题目内容
若平面四边形ABCD满足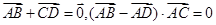 ,则该四边形一定是( )
,则该四边形一定是( )
| A.正方形 | B.矩形 | C.菱形 | D.直角梯形 |
C
解析试题分析:因为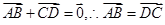 ,所以四边形ABCD为平行四边形,又因为
,所以四边形ABCD为平行四边形,又因为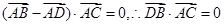 ,所以BD垂直AC,所以四边形ABCD为菱形.
,所以BD垂直AC,所以四边形ABCD为菱形.
考点:向量在证明菱形当中的应用.
点评:在利用向量进行证明时,要注意向量平行与直线平行的区别,向量平行两条直线可能共线也可能平行.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
在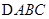 中,已知
中,已知 ,则|
,则|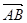 |的值为( )
|的值为( )
| A.1 | B.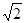 | C.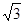 | D.2 |
如图, 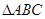 中,
中, 、
、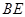 、
、 分别是
分别是 、
、 、
、 上的中线, 它们交于点
上的中线, 它们交于点 ,则下列各等式中不正确的是 ( )
,则下列各等式中不正确的是 ( ) 
A.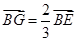 | B. ; ; |
C. | D.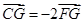 |
若 为任意向量,m∈R,则下列等式不一定成立的是
为任意向量,m∈R,则下列等式不一定成立的是
A. = = | B. = = |
C.m( )=m )=m | D. = = |
设 不共线,则下列四组向量中不能作为基底的是( )
不共线,则下列四组向量中不能作为基底的是( )
A. 与 与 | B. 与 与 |
C.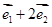 与 与 | D. 和 和 |
已知 ,点
,点 在直线
在直线 上,且
上,且 ,则点
,则点 的坐标为( )
的坐标为( )
A.( | B.(8,-15) |
C. ( )或 )或 | D.( )或(6,-9) )或(6,-9) |
若四边形 满足
满足 ,
, ,则该四边形一定是
,则该四边形一定是
| A.直角梯形 | B.菱形 | C.矩形 | D.正方形 |
化简 ( ).
( ).
A. | B. | C. | D. |
 ,则
,则 的值
的值
 B.
B. C.
C. D.
D.