题目内容
设 不共线,则下列四组向量中不能作为基底的是( )
不共线,则下列四组向量中不能作为基底的是( )
A. 与 与 | B. 与 与 |
C.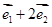 与 与 | D. 和 和 |
B
解析试题分析:∵ =-2(
=-2( ),∴(
),∴( )∥(
)∥( ),故
),故 与
与 不能作为基底,故选B
不能作为基底,故选B
考点:本题考查了基底的概念
点评:熟练掌握基底的概念及共线向量的判定是求解此类问题的关键,属基础题

练习册系列答案
相关题目
在 所在的平面内,点
所在的平面内,点 满足
满足 ,
, ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
 ,则( )
,则( )
A. | B. | C.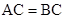 | D. |
设 是两个非零向量,下列选项正确的是( )
是两个非零向量,下列选项正确的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则存在实数 ,则存在实数 ,使得 ,使得 |
D.若存在实数 ,使得 ,使得 ,则 ,则 |
以下说法错误的是( )
| A.零向量与任一非零向量平行 | B.零向量与单位向量的模不相等 |
| C.平行向量方向相同 | D.平行向量一定是共线向量 |
设 ,
, ,
,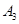 ,
, 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称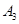 ,
, 调和分割
调和分割 ,
, ,已知点C(c,0),
,已知点C(c,0),
D(d,0) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
| A.C可能是线段AB的中点 | B.D可能是线段AB的中点 |
| C.C,D可能同时在线段AB上 | D.C,D不可能同时在线段AB的延长线上 |
若平面四边形ABCD满足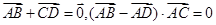 ,则该四边形一定是( )
,则该四边形一定是( )
| A.正方形 | B.矩形 | C.菱形 | D.直角梯形 |
已知单位向量 满足
满足 ,则
,则 夹角为( )
夹角为( )
A. | B. | C. | D. |
若 为
为 所在平面内一点,且满足
所在平面内一点,且满足 ,
,
则 的形状为( )
的形状为( )
| A.等腰三角形 | B.直角三角形 | C.正三角形 | D.等腰直角三角形 |