题目内容
已知n为正偶数，用数学归纳法证明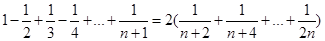
时，若已假设
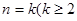为偶数）时命题为真，则还需要用归纳假设再证
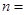（ ）时等式成立 （ ）
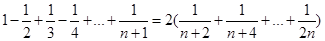时，若已假设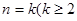为偶数）时命题为真，则还需要用归纳假设再证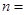（ ）时等式成立 （ ）A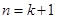． | B． | C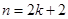． | D． |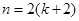
B
试题分析：首先分析题目因为n为正偶数，用数学归纳法证明的时候，若已假设n=k（k≥2，k为偶数）时命题为真时，因为n取偶数，则n=k+1代入无意义，故还需要证明n=k+2成立．
若已假设n=k（k≥2，k为偶数）时命题为真，因为n只能取偶数，所以还需要证明n=k+2成立．故选B．
点评：此题主要考查数学归纳法的概念问题，对学生的理解概念并灵活应用的能力有一定的要求，属于基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
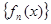满足：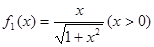
，
；
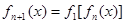
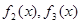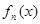的表达式，并证明你的结论.
＋…＋
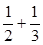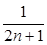(n∈N*)中，当n＝1时式子值为1＋
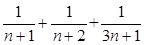(n∈N*)，则f(k＋1)＝f(k)＋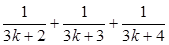
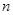条两两相交的弦，把圆最多分成 部分.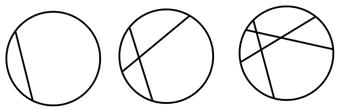
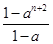(n∈N*，a≠1)，在验证n＝1时，左边所得的项为（ ）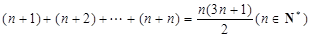
，
，
，
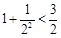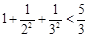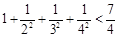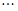则可归纳出式子（ ）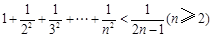
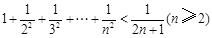
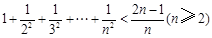
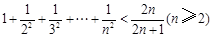
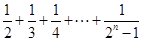，则n=k+1与n=k时相比，左边应添加( )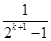
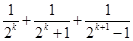
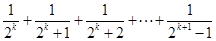
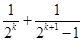
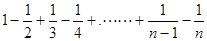（n为正偶数），从“n=2k”到“n=2k+2”左边需增加的代数式为________.