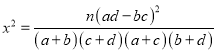题目内容
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见证明
【解析】
(Ⅰ)利用导数与函数单调性的关系求解;
(Ⅱ)af(x)>lnx![]() .令F(x)
.令F(x)![]() ,F′(x)
,F′(x)![]() (x>0).
(x>0).
①当∈(0,1]时,F′(x)<0,F(x)单调递减,F(x)≥F(1)=ae>0;
②当>1时,令G(x)![]() ,利用导数求得最小值大于0即可.
,利用导数求得最小值大于0即可.
解.(1)f(x)的定义域为(﹣∞,0)∪(0,+∞),
∵![]() ,
,
∴x∈(﹣∞,0),(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0
∴函数f(x)的单调增区间为:(1,+∞),减区间为(﹣∞,0),(0,1).
(2)af(x)>lnx![]() .
.
令F(x)![]() ,
,
F′(x)![]() .(x>0).
.(x>0).
①当x∈(0,1]时,F′(x)<0,F(x)单调递减,F(x)≥F(1)=ae>0;
②当x>1时,令G(x)![]() ,G
,G![]() .
.
∴G(x)在(1,+∞)单调递增,
∵x→1时,G(x)→﹣∞,G(2)=e2![]() 0,
0,
∴G(x)存在唯一零点0∈(1,2),
F(x)min=F(x0)![]()
∵G(x0)=0,![]() .
.
综上所述,当![]() 时,af(x)>lnx成立.
时,af(x)>lnx成立.

练习册系列答案
相关题目