题目内容

【题目】选修4-5：不等式选讲
设函数f（x）=|x﹣1|﹣|2x+1|的最大值为m．
（1）作出函数f（x）的图象；
（2）若a2+2c2+3b2=m，求ab+2bc的最大值．

【答案】
（1）解：当x≤﹣ 时，f（x）=（1﹣x）+2x+1=x+2；

当﹣ ＜x＜1时，f（x）=（1﹣x）﹣2x﹣1=﹣3x：

当x≥1时，f（x）=（x﹣1）﹣2x﹣1=﹣x﹣2，

函数f（x）的图象，如图所示

；


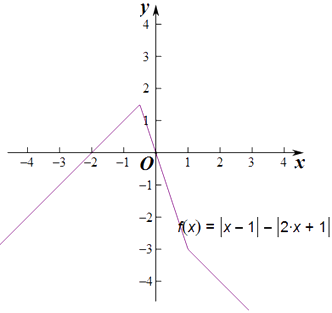（2）解：由题意，当x=﹣ 时，f（x）取得最大值m=1.5，∴a2+2c2+3b2=1.5，

∴ab+2bc≤ （a2+2c2+3b2）= ，即ab+2bc的最大值为 ．


【解析】（1）分类讨论，作出函数f（x）的图象；（2）求出函数的值域，即可求m的值，利用基本不等式求ab+2bc的最大值．

练习册系列答案
相关题目

【题目】已知f（x）是定义在R上的奇函数，当x＞0时，f（x）= x3+ax（a∈R），且曲线f（x）在x= 处的切线与直线y=﹣ x﹣1平行．
（Ⅰ）求a的值及函数f（x）的解析式；
（Ⅱ）若函数y=f（x）﹣m在区间[﹣3， ]上有三个零点，求实数m的取值范围．

【题目】过双曲线 的右支上的一点P作一直线l与两渐近线交于A、B两点，其中P是AB的中点；
（1）求双曲线的渐近线方程；
（2）当P坐标为（x0 ， 2）时，求直线l的方程；
（3）求证：|OA||OB|是一个定值．

【题目】已知等差数列{an}的前n项和为Sn ， 若Sm﹣1=﹣4，Sm=0，Sm+2=14（m≥2，且m∈N*）．
（1）求m的值；
（2）若数列{bn}满足 =logabn（n∈N*），求数列{（an+6）bn}的前n项和．

【题目】已知常数λ≥0，设各项均为正数的数列{an}的前n项和为Sn，满足：a1 = 1，

（）．

(1)若λ = 0，求数列{an}的通项公式；

(2)若对一切恒成立，求实数λ的取值范围．

【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c，已知a≠b，c= ，且bsinB﹣asinA= acosA﹣ bcosB．
（Ⅰ）求C；
（Ⅱ）若△ABC的面积为 ，求a与b的值．

【题目】设双曲线x2－＝1上有两点A，B，AB中点M(1，2)，求直线AB的方程．

【题目】已知椭圆的左、右焦点分别为F1(－c，0)，F2(c，0)，直线交椭圆E于A，B两点，△ABF1的周长为16，△AF1F2的周长为12．

(1)求椭圆E的标准方程与离心率；

(2)若直线l与椭圆E交于C，D两点，且P(2，2)是线段CD的中点，求直线l的一般方程．

【题目】直线l：ax+ y﹣1=0与x，y轴的交点分别为A，B，直线l与圆O：x2+y2=1的交点为C，D．给出下列命题：p：a＞0，S△AOB= ，q：a＞0，|AB|＜|CD|．则下面命题正确的是（ ）
A.p∧q
B.￢p∧￢q
C.p∧￢q
D.￢p∧q

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网