Question

已知直线l的参数方程是

x=2t y=4t+a

（t为参数），圆C的极坐标方程为ρ=4

2

cos（θ+

π

4

）．
（Ⅰ）将圆C的极坐标方程化写为直角坐标系方程；
（Ⅱ）若圆C上有且仅有三个点到直线l距离为

2

，求实数a的值．

Answer 1

分析：（Ⅰ）利用极坐标系与直角坐标系的互化公式即可得出；
（Ⅱ）要满足条件“圆C上有且仅有三个点到直线l距离为

2

”，当圆心C到直线l的距离为

2

时即可．

解答：解：（Ⅰ）由圆C的极坐标方程为ρ=4

2

cos（θ+

π

4

）展开得ρ=4cosθ-4sinθ，变为ρ²=4ρcosθ-4ρsinθ，
化为直角坐标系方程x²+y²=4x-4y，
∴圆C的直角坐标系方程为x²+y²=4x-4y；
（Ⅱ）直线l的参数方程是

x=2t y=4t+a

（t为参数），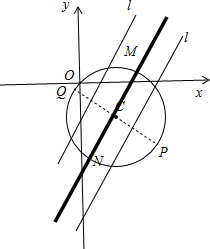
消去参数化为y=2x+a．
由（1）可知：圆C的方程为（x-2）²+（y+2）²=8，
∴圆心C（2，-2），半径r=2

2

．
如图所示：
∵圆C上有且仅有三个点到直线l距离为

2

，半径r=2

2

．
∴当圆心C到直线l的距离为

2

时，与直线l平行的直径与圆的两个交点满足条件，另外与直线l平行且与圆相切的切线的切点也满足条件，因此圆C上共有三个点到直线l的距离等于

2

．
∴

|4+2+a|

22+(-1)2

=

2

，解得a=-6±

10

．
∴实数a的值为-6±

10

．

点评：熟练掌握极坐标系与直角坐标系的互化公式、点到直线的距离公式及把问题等价转化是解题的关键．