题目内容
极坐标与参数方程:
已知直线l的参数方程是:
(t为参数),圆C的极坐标方程是:ρ=2
sin(θ+
),试判断直线l与圆C的位置关系.
已知直线l的参数方程是:
|
| 2 |
| π |
| 4 |
分析:将直线l化成普通方程,得2x-y+1=0.再将圆C化成普通方程:x2+y2-2x-2y=0,得到圆心为点C(1,1),半径r=
,最后求出点C到直线l的距离d小于半径r,得到直线l与圆C相交.
| 2 |
解答:解:将直线l:
(t为参数),化成普通方程得2x-y+1=0
∵圆C的极坐标方程是:ρ=2
sin(θ+
),即ρ=2sinθ+2cosθ
∴两边都乘以ρ,得ρ2=2ρsinθ+2ρcosθ
结合
,可得圆C的普通方程是:x2+y2=2x+2y,即x2+y2-2x-2y=0,
∴圆C是以点C(1,1)为圆心,半径r=
的圆.
∵点C到直线l:2x-y+1=0的距离为d=
=
<
∴直线l与圆C相交.
|
∵圆C的极坐标方程是:ρ=2
| 2 |
| π |
| 4 |
∴两边都乘以ρ,得ρ2=2ρsinθ+2ρcosθ
结合
|
∴圆C是以点C(1,1)为圆心,半径r=
| 2 |
∵点C到直线l:2x-y+1=0的距离为d=
| 2 | ||
|
| 2 |
| 5 |
| 5 |
| 2 |
∴直线l与圆C相交.
点评:本题以直线与圆的位置关系为例,着重考查了直线的参数方程、圆的极坐标方程和参数方程、极坐标方程与普通方程互化等知识点,属于中档题.

练习册系列答案
相关题目
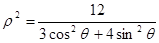 ,点
,点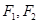 为其左,右焦点,直线
为其左,右焦点,直线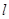 的参数方程为
的参数方程为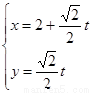 (
(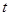 为参数,
为参数,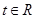 ).
). ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (t是参数)。
(t是参数)。