题目内容
（本小题满分12分）
已知椭圆的一个焦点为F1(-1,0)，对应的准线方程为
，且离心率e满足：
成等差数列。
（1）求椭圆C方程；
（2）如图，抛物线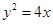
的一段与椭圆C的一段围成封闭图形，点N（1，0）在x轴上，又A、B两点分别在抛物线及椭圆上，且AB//x轴，求△NAB的周长
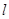的取值范围。
【答案】
解：（1）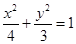
………………4分
（2）易知N为抛物线y2=4x的焦点，又为椭圆的右焦点，
抛物线的准线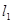
：x=-1，椭圆的右准线l2：x=4，
过A作AC^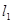于C，过B作BD^
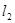于D，
则C、A、B、D在同一条与x轴平行的直线上。
由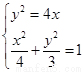
，得抛物线与椭圆的交点M的横坐标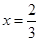
而|BN|=e|BD|=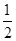
|BD|,|AN|=|AC|
∴△NAB的周长l=|AN|+|AB|+|NB|=|BC|+|BN|
=|BC|+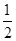|BD|=|BC|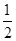+|BD|-|BD|
=|CD|-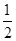|BD|=5-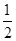|BD|
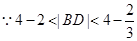，即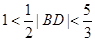
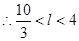，即l的取值范围为（
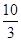，4）………………12分
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
