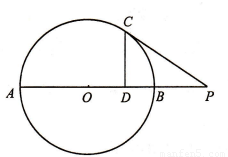
题目内容
 如图,自⊙O外一点P作⊙O的切线PC和割线PBA,点C切点,割线PBA交⊙O于A、B两点,点O在AB上,作CD⊥AB,垂足为点D.求证:
如图,自⊙O外一点P作⊙O的切线PC和割线PBA,点C切点,割线PBA交⊙O于A、B两点,点O在AB上,作CD⊥AB,垂足为点D.求证:| PC |
| PA |
| BD |
| DC |
分析:连结BC、AC,由弦切角定理得∠PCB=∠PAC,△PCB∽△PAC,可得
=
.根据AB是圆O的直径,得到Rt△ABC中CD⊥AB,所以△BDC∽△CDA,可得
=
,从而可得
=
成立.
| PC |
| PA |
| BC |
| AC |
| BD |
| DC |
| BC |
| AC |
| PC |
| PA |
| BD |
| DC |
解答:解:连结BC、AC,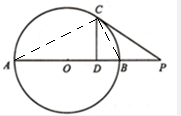
∵PC切⊙O于点C,∴∠PCB=∠PAC,
又∵∠BPC=∠CPA,∴△PCB∽△PAC,可得
=
…①,
∵AB是圆O的直径,∴AC⊥BC.
∵Rt△ABC中,CD⊥AB
∴△BDC∽△CDA,可得
=
…②,
比较①②,可得
=
.

∵PC切⊙O于点C,∴∠PCB=∠PAC,
又∵∠BPC=∠CPA,∴△PCB∽△PAC,可得
| PC |
| PA |
| BC |
| AC |
∵AB是圆O的直径,∴AC⊥BC.
∵Rt△ABC中,CD⊥AB
∴△BDC∽△CDA,可得
| BD |
| DC |
| BC |
| AC |
比较①②,可得
| PC |
| PA |
| BD |
| DC |
点评:本题给出圆的直径与切线,求证对应线段成比例.着重考查了圆的直径的性质、弦切角定理、相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分.
选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分. (2012•江苏二模)选做题
(2012•江苏二模)选做题
 .
.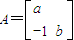 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值. =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.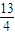 ,求x+y+z的最大值.
,求x+y+z的最大值.