题目内容
函数y=loga（x2-ax+2）在[2，+∞）上恒为正，则实数a的取值范围是
- A.0＜a＜1
- B.1＜a＜2
- C.
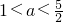
- D.2＜a＜3
B
分析：函数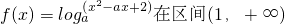
上恒为正值等价于当x＞1时，f（x）=loga（x2-ax+2）＞loga1．然后再分0＜a＜1和a＞1两种情况分别讨论，计算可得答案．
解答：∵函数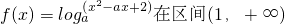上恒为正值，∴当x＞1时，f（x）=loga（x2-ax+2）＞loga1．
当0＜a＜1时，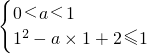
，此方程组无解；当a＞1时，
，
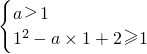解得1＜a≤2．
故选B．
点评：在解对数函数时，当a的范围没有明确时，必须分0＜a＜1和a＞1两种情况分别讨论．
分析：函数
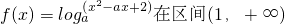上恒为正值等价于当x＞1时，f（x）=loga（x2-ax+2）＞loga1．然后再分0＜a＜1和a＞1两种情况分别讨论，计算可得答案．解答：∵函数
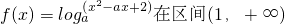上恒为正值，∴当x＞1时，f（x）=loga（x2-ax+2）＞loga1．当0＜a＜1时，
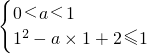，此方程组无解；当a＞1时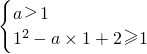，，解得1＜a≤2．
故选B．
点评：在解对数函数时，当a的范围没有明确时，必须分0＜a＜1和a＞1两种情况分别讨论．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
12、已知函数y=loga（x+b）的图象如图所示，则ba=
已知函数y=loga（x+3）-1（a＞0且a≠1）的图象恒过定点A，若点A也在函数f（x）=3x+b的图象上，则f（log94）=（ ）