题目内容
等差数列{an}中,a2=4,其前n项和Sn满足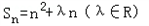 .
.
(I)求实数λ的值,并求数列{an}的通项公式;
(II)若数列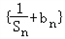 是首项为λ、公比为2λ的等比数列,求数列{bn}的前n项的和Tn.
是首项为λ、公比为2λ的等比数列,求数列{bn}的前n项的和Tn.
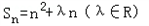 .
.(I)求实数λ的值,并求数列{an}的通项公式;
(II)若数列
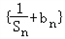 是首项为λ、公比为2λ的等比数列,求数列{bn}的前n项的和Tn.
是首项为λ、公比为2λ的等比数列,求数列{bn}的前n项的和Tn.解:(I)因为a2=S2﹣S1=4+2λ﹣1﹣λ=4,解得λ=1
∴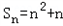
当n≥2时,则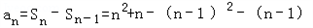 =2n,
=2n,
当n=1时,也满足,
所以an=2n.
(II)由已知数列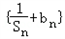 是首项为1、公比为2的等比数列
是首项为1、公比为2的等比数列
其通项公式为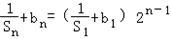 ,且首项
,且首项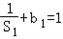 ,
,
故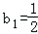 ,
,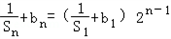 =2n﹣1
=2n﹣1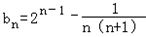 =
=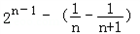 ,
,
Tn =(1+21+…+2n-1)…﹣[(1﹣ )+(
)+(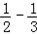 )+…+(
)+…+(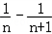 )]=2n﹣1﹣
)]=2n﹣1﹣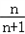 .
.
∴
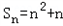
当n≥2时,则
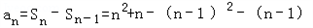 =2n,
=2n,当n=1时,也满足,
所以an=2n.
(II)由已知数列
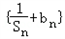 是首项为1、公比为2的等比数列
是首项为1、公比为2的等比数列其通项公式为
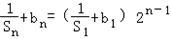 ,且首项
,且首项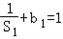 ,
,故
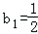 ,
,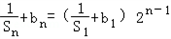 =2n﹣1
=2n﹣1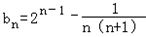 =
=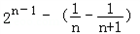 ,
,Tn =(1+21+…+2n-1)…﹣[(1﹣
 )+(
)+(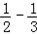 )+…+(
)+…+(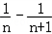 )]=2n﹣1﹣
)]=2n﹣1﹣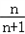 .
.
练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目