题目内容
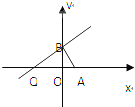 已知A(
已知A(| 1 |
| 4 |
| AP |
| AQ |
| AB |
(1)求点P的轨迹方程;
(2)是否存在定直线x=a,以PM为直径的圆与直线x=a的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由.
分析:(1)由题意设出B,Q的坐标,利用直角三角形中的射影定理得到B,Q坐标的关系,然后结合题目给出的向量等式列式,消掉参数后即可求得点P的轨迹方程;
(2)因为P在(1)中的抛物线上,设出P的坐标,求出PM的中点坐标,利用弦心距公式列式求出以PM为直径的圆与直线x=a的相交弦长,有现场为定值可求得定值a的值.
(2)因为P在(1)中的抛物线上,设出P的坐标,求出PM的中点坐标,利用弦心距公式列式求出以PM为直径的圆与直线x=a的相交弦长,有现场为定值可求得定值a的值.
解答:解:(1)设B(0,t),设Q(m,0),t2=
|m|,∵m≤0,∴m=-4t2,
∴Q(-4t2,0),设P(x,y),则
=(x-
,y),
=(-4t2-
,0),
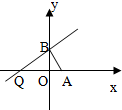
2
=(-
,2t),∵
+
=2
.
∴(x-
,y)+(-4t2-
,0)=(-
,2t),
∴x=4t2,y=2t,∴y2=x,此即点P的轨迹方程;
(2)存在定直线x=
,以PM为直径的圆与直线x=
的相交弦长为定值
.
事实上,由(1)知点P的轨迹方程是y2=x.
设P(y2,y),∵M (4,0),
则以PM为直径的圆的圆心即PM的中点T(
,
),
以PM为直径的圆与直线x=a的相交弦长:
L=2
=2
=2
若a为常数,则对于任意实数y,L为定值的条件是a-
=0,即a=
时,L=
.
∴存在定直线x=
,以PM为直径的圆与直线x=
的相交弦长为定值
.
| 1 |
| 4 |
∴Q(-4t2,0),设P(x,y),则
| AP |
| 1 |
| 4 |
| AQ |
| 1 |
| 4 |

2
| AB |
| 1 |
| 2 |
| AP |
| AQ |
| AB |
∴(x-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴x=4t2,y=2t,∴y2=x,此即点P的轨迹方程;
(2)存在定直线x=
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
事实上,由(1)知点P的轨迹方程是y2=x.
设P(y2,y),∵M (4,0),
则以PM为直径的圆的圆心即PM的中点T(
| y2+4 |
| 2 |
| y |
| 2 |
以PM为直径的圆与直线x=a的相交弦长:
L=2
(
|
=2
(a-4)(y2-a)+
|
(a-
|
若a为常数,则对于任意实数y,L为定值的条件是a-
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
∴存在定直线x=
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
点评:本题考查了与直线有关的动点轨迹方程的求法,考查了直线与圆的关系,训练了利用弦心距求弦长,是有一定难度题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点F(-
,0),直线l:x=
,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是( )
| 1 |
| 4 |
| 1 |
| 4 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |