题目内容

已知点F(
1
4
，0)，直线l：x=-
1
4
，点B是l上的动点．若过B垂直于y轴的直线与线段BF的垂直平分线交于点M，则点M的轨迹是（　　）
分析：由题意画出图形，通过转化判断点M的轨迹即可．
解答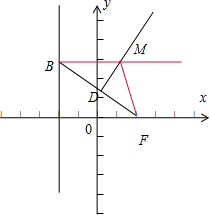：解：如图，因为点F(
1
4
，0)，直线l：x=-
1
4
，点B是l上的动点．
若过B垂直于y轴的直线与线段BF的垂直平分线交于点M，
所以MF=MB，MB⊥l，
所以M的轨迹满足抛物线的定义，所以轨迹为抛物线，
故选D．
点评：本题考查曲线轨迹方程的求法，抛物线的定义的应用，考查基本知识的应用．
练习册系列答案
相关题目
已知点C(
1
4
，0)，椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右准线l1+x=2与x轴相交于点D，右焦点F到上顶点的距离为
2
．
（1）求椭圆的方程；
（2）是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点，使得(
CA
+
CB
)⊥
BA
？若存在，求出直线l；若不存在，说明理由．
已知点F(
1
4
，0)，直线l：x=-
1
4
，点B是l上的动点，若过B垂直于y轴的直线与线段BF的垂直平分线交于点M，则点M的轨迹方程是
 
．
已知点F(-
1
4
，0)，直线l：x=
1
4
，点B是直线l上的动点，若过B垂直于y轴的直线与线段BF的垂直平分线交于点M，则点M所在曲线是（　　）
A、圆B、椭圆C、双曲线D、抛物线
已知点F(-
1
4
，0)，直线l：x=
1
4
，点B是直线l上的动点，若过B垂直于y轴的直线与线段BF的垂直平分线交于点M，则点M所在曲线是（　　）
A．圆B．椭圆C．双曲线D．抛物线

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网