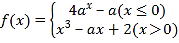Question

【题目】已知函数

（1）当时，求的极大值；

（2）讨论的单调区间；

（3）对任意的，不等式恒成立，求的取值范围．

Answer 1

【答案】（1）；（2）单调递增区间是(－∞,a－2)，(a,＋∞)，单调递减区间是(a－2,a)；（3）.

【解析】

（1）求导，令导数为零，讨论函数的单调性，即可根据单调性求得极大值；

（2）求导，对导数分解因式，列表，写出函数的单调区间即可；

（3）对参数进行分类讨论，考虑每种情况下函数在区间上的最值，根据不等式恒成立，求得参数的取值范围.

（1）时，

则，

令解得或.

当时，；

当时，；

当时，；

所以时，有极大值，

极大值为

（2）f(x)＝2(x－a)ex＋(x－a)2ex＝(x－a) [x－(a－2)]ex．

令f(x)＝0，．

当x变化时，f(x)、f(x)的变化如下：

x	(－∞,a－2)	a－2	(a－2,a)	a	(a,＋∞)
f(x)	＋	0	－	0	＋
f(x)	↗	极大值	↘	极小值	↗

所以f(x)的单调递增区间是(－∞，a－2)，(a，＋∞)，单调递减区间是(a－2，a)．

（3）由（2）得f(x)的极大值为f(a－2)＝4ea－2．

（i）当a≤1时，

f(x)在(－∞,1]上的最大值为f(a－2)或f(1)，

即可得，且，

解得，且，

结合，

解得满足题意的；

（ii）当 即时，

f(x)在(－∞，1]上的最大值为f(a－2)

此时f(a－2)满足题意，

故.

（iii）当时，即，

的最大值为，

又，

故不恒成立

综上，的取值范围是