题目内容
【题目】函数![]() 中,
中,![]() 满足对
满足对![]() 有
有![]() ,当
,当![]() 时,
时,![]() ;函数
;函数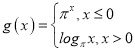 ;函数
;函数![]() .现给出
.现给出![]() 是偶函数;
是偶函数;![]() 在
在![]() 上单调递增;
上单调递增;![]() 无最大值;
无最大值;![]() 有
有![]() 个零点这四个结论,则正确结论的编号是( )
个零点这四个结论,则正确结论的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由条件![]() 满足对
满足对![]() 有
有![]() ,
,![]() 时,
时,![]() ,
,
可得函数![]() 的图像特点,再结合
的图像特点,再结合![]() 的表达式,对4个命题进行逐一判断,即可找出正确的命题,得到答案.
的表达式,对4个命题进行逐一判断,即可找出正确的命题,得到答案.
![]() 满足对
满足对![]() 有
有![]() ,
,![]() 时,
时,![]()
将![]() 在
在![]() 上的图像向右平移个
上的图像向右平移个![]() 单位,再将纵坐标扩到为原来的2倍,得到
单位,再将纵坐标扩到为原来的2倍,得到![]() 上的图像.
上的图像.
将![]() 在
在![]() 上的图像向右平移个
上的图像向右平移个![]() 单位,再将纵坐标扩到为原来的2倍,得到
单位,再将纵坐标扩到为原来的2倍,得到![]() 上的图像.
上的图像.
将![]() 在
在![]() 上的图像向左平移个
上的图像向左平移个![]() 单位,再将纵坐标变为为原来的
单位,再将纵坐标变为为原来的![]() ,得到
,得到![]() 上的图像,
上的图像,
依此类推可得![]() 的图像,如图.
的图像,如图.
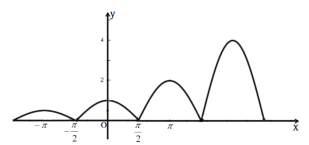
所以![]() 不是周期函数,所以
不是周期函数,所以![]() 错误.
错误.
由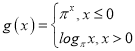 ,作出其函数图像,如图.
,作出其函数图像,如图.
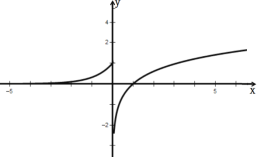
由图显然![]() 在
在![]() 上不是单调递增函数,所以
上不是单调递增函数,所以![]() 错误.
错误.
当![]() 大于0,且
大于0,且![]() 时,
时,![]() .
.
所以当![]() 大于0,且
大于0,且![]() 时
时![]() .
.
所以![]() 无最大值,故
无最大值,故![]() 正确.
正确.
函数![]() 的零点个数,即函数
的零点个数,即函数![]() 与
与![]() 图像的在
图像的在![]() 上交点的个数.
上交点的个数.
作出函数![]() 与
与![]() 的图像,如同
的图像,如同
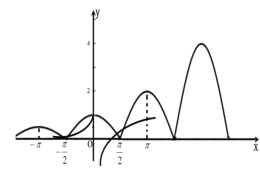
由图像可知, 函数![]() 与
与![]() 图像的在
图像的在![]() 上有5个交点,故
上有5个交点,故![]() 正确.
正确.
故选: D

 阅读快车系列答案
阅读快车系列答案【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%