题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 在
在![]() 上且其横坐标为1,以
上且其横坐标为1,以![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 的准线相切.
的准线相切.
(1)求![]() 的值;
的值;
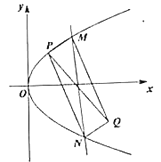
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,若点
,若点![]() 关于
关于![]() 的对称点在
的对称点在![]() 上,求
上,求![]() 的方程.
的方程.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)本题可以根据“点![]() 到准线的距离”等于“点
到准线的距离”等于“点![]() 到焦点的距离”得出
到焦点的距离”得出![]() 的长,再根据“圆心
的长,再根据“圆心![]() 到准线的距离”以及“点
到准线的距离”以及“点![]() 到焦点的距离”都是圆的半径即可列出算式并得出结果;
到焦点的距离”都是圆的半径即可列出算式并得出结果;
(2)首先可以根据题意画出图形,然后设出直线![]() 的方程以及直线
的方程以及直线![]() 的方程,再然后通过联立方程组求出点
的方程,再然后通过联立方程组求出点![]() 的纵坐标以及点
的纵坐标以及点![]() 的纵坐标之和,最后通过
的纵坐标之和,最后通过![]() 计算出点
计算出点![]() 的纵坐标并与点
的纵坐标并与点![]() 的纵坐标进行比较即可计算出
的纵坐标进行比较即可计算出![]() 的值并得出结果。
的值并得出结果。
(1)圆心![]() 到准线的距离为
到准线的距离为![]() ,因为点
,因为点![]() 的横坐标为1,所以
的横坐标为1,所以![]() ,
,
依题意,有![]() ,所以
,所以![]() 。
。
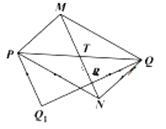
(2)如图所示,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,线段
,线段![]() 与直线
与直线![]() 的交点为
的交点为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
将点![]() 的横坐标为
的横坐标为![]() 带入抛物线方程
带入抛物线方程![]() 中可得
中可得![]() ,
,
因为![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,所以
的中点,所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立方程组![]() ,得
,得![]() ,
,
因为![]() 是该方程的一个根,所以它的另一个根为
是该方程的一个根,所以它的另一个根为![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() .
.
联立方程组![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
设![]() ,因为
,因为![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
即![]() ,
,
所以![]() ,即
,即![]() .
.
所以点![]() 与点
与点![]() 的纵坐标相等,
的纵坐标相等,![]() 轴,
轴,
因为![]() ,所以
,所以![]() ,
,![]() 的方程为
的方程为![]() 。
。

【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:31 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:59 | 12月20日 | 7:31 |
表2:某年2月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(Ⅰ)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(Ⅱ)甲,乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立.记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(Ⅲ)将表1和表2中的升旗时刻化为分数后作为样本数据(如7:31化为![]() ).记表2中所有升旗时刻对应数据的方差为
).记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【题目】国家统计局进行第四次经济普查,某调查机构从15个发达地区,10个欠发达地区,5个贫困地区中选取6个作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 90 | 60 | 150 |
合计 | 130 | 70 | 200 |
(1)写出选择6个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有97.5%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”,分析造成这个结果的原因并给出合理化建议.
附:参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
