题目内容
随机在圆O:x2+y2=1内投一个点A,则点A刚好落在不等式组
围成的区域内的概率是( )
|
分析:先分别画出不等式组表示的区域,然后分别求面积,根据几何概型的知识即可得解.
解答: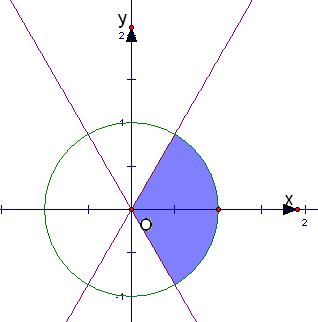 解:平面区域Ω表示的是单位圆及其内部,区域M表示的是阴影部分,如图所示:
解:平面区域Ω表示的是单位圆及其内部,区域M表示的是阴影部分,如图所示:
又∵区域Ω的面积为:S1=πR2=π×12=π
区域M的面积为:S2=
×
×1=
∴点A刚好落在不等式组围成的区域内的概率是
.
故选B.
 解:平面区域Ω表示的是单位圆及其内部,区域M表示的是阴影部分,如图所示:
解:平面区域Ω表示的是单位圆及其内部,区域M表示的是阴影部分,如图所示:又∵区域Ω的面积为:S1=πR2=π×12=π
区域M的面积为:S2=
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 3 |
∴点A刚好落在不等式组围成的区域内的概率是
| 1 |
| 3 |
故选B.
点评:本题考查一元二次不等式组表示的区域以及几何概型,须准确画图并求面积.属简单题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )
如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )