题目内容
如图，已知函数y=sinx，x∈[-π，π]与x轴围成的区域记为M（图中阴影部分），若随机向圆O：x2+y2=π2内投入一米粒，则该米粒落在区域M内的概率是（ ）分析：先计算阴影部分面积、圆O：x2+y2=π2的面积，再以面积为测度，可得该米粒落在区域M内的概率．
解答：解：先计算阴影部分面积S=
sinxdx=2（-cosx）
=4，圆O：x2+y2=π2的面积为π2，
再以面积为测度，可得该米粒落在区域M内的概率是
故选A．
| 2∫ | π 0 |
| | | π 0 |
再以面积为测度，可得该米粒落在区域M内的概率是
| 4 |
| π2 |
故选A．
点评：本题考查几何概型，考查利用定积分计算面积，解题的关键是确定阴影的面积．
练习册系列答案
全能测控一本好卷系列答案
相关题目
（2012•江西）如图，已知正四棱锥S-ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（ ）
（2007•广州一模）如图，已知曲线C1：y=x2与曲线C2：y=-x2+2ax（a＞1）交于点O，A，直线x=t（0＜t≤1）与曲线C1，C2分别相交于点D，B，连结OD，DA，AB，OB．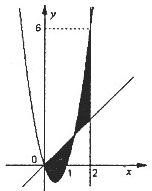
如图，已知二次函数f（x）=ax2+bx+c，直线l1：x=2，直线l2：y=3tx（其中-1＜t＜1，t为常数）；若直线l2与函数f（x）的图象以及直线l1，l2与函数f（x）以及的图象所围成的封闭图形如阴影所示．
如图，已知矩形ABCD的一边AB在x轴上，另两个顶点C，D落在抛物线弧y=-x2+2x（0＜x＜2）上．设点C的横坐标为x．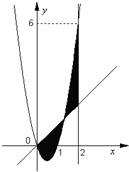
如图，已知二次函数f（x）=ax2+bx+c，直线l1：x=2，直线l2：y=3tx（其中-1＜t＜1，t为数）；．若直线l2与函数f（x）的图象以及直线l1，l2与函数f（x）的图象所围成的封闭图形如阴影所示．