题目内容
【题目】已知定义在R上的奇函数,当x>0时,f(x)=x2+2x﹣1
(1)求f(﹣3)的值;
(2)求函数f(x)的解析式.
【答案】
(1)解:因为定义在R上的奇函数f(x),满足当x>0时,f(x)=x2+2x﹣1,
所以f(﹣3)=﹣f(3)=﹣(9+6﹣1)=﹣14
(2)解:因为定义在R上的奇函数f(x),
所以f(﹣0)=﹣f(0),即f(0)=0,
设x<0,则﹣x>0,
因为当x>0时,f(x)=x2+2x﹣1,
所以f(﹣x)=x2﹣2x﹣1=﹣f(x),
即当x<0时,f(x)=﹣x2+2x+1,
综上得,f(x)= 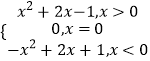
【解析】(1)根据题意和奇函数的性质求出f(﹣3)的值;(2)根据奇函数的性质可得f(0)=0,设x<0则﹣x>0,由条件和奇函数的性质求出x<0的表达式,再用分段函数表示出来即可.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 ![]() 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及下面一些统计量的值.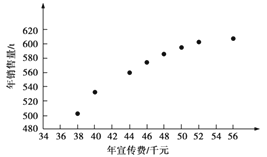
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中 ![]() ,
, ![]() .
.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最下二乘估计分别为 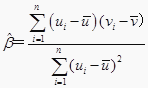 ,
, ![]() .
.
(1)根据散点图判断,y=a+bx与 ![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
①年宣传费x=49时,年销售量及年利润的预报值时多少?
②年宣传费x为何值时,年利润的预报值最大?
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.
的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.

(1)由拆线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系.求
之间的关系.求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 公司2017年4月份(即
公司2017年4月份(即![]() 时)的市场占有率;
时)的市场占有率;
(2)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的![]() 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 报废年限 | 1年 | 2年 | 3年 | 4年 | 总计 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年,且以频率作为每辆单车使用寿命的概率.如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
(参考公式:回归直线方程为![]() ,其中
,其中 )
)