题目内容
已知函数f(x)=lg(ax-kbx )(k是正实数,a>1>b>0)的定义域为(0,+∞),问是否存在实数a,b,当x∈(1,+∞)时,f(x)的值取到一切正实数,且f(3)=lg4;如果存在,求出a,b的值;如果不存在,请说明理由。
不存在
设存在这样的实数a、b满足条件。
由ak-bk>0得(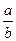 )x>k,因为a>1>b>0 所以x>log
)x>k,因为a>1>b>0 所以x>log =0,k=1
=0,k=1
所以f(x)=lg(ak-bk),又f(x)恰好在(1,+∞)上
取正值,且f(x)在(1,+∞)上为增函数。故f(1)=0
f(3)=lg4,所以 所以a=
所以a=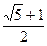 ,b=
,b= ,故这样的a、b存在
,故这样的a、b存在
由ak-bk>0得(
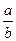 )x>k,因为a>1>b>0 所以x>log
)x>k,因为a>1>b>0 所以x>log =0,k=1
=0,k=1所以f(x)=lg(ak-bk),又f(x)恰好在(1,+∞)上
取正值,且f(x)在(1,+∞)上为增函数。故f(1)=0
f(3)=lg4,所以
 所以a=
所以a=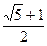 ,b=
,b= ,故这样的a、b存在
,故这样的a、b存在
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
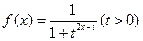 .
.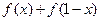 为定值;
为定值;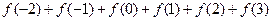 的值.
的值.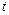 元(其中
元(其中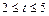 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为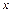 元(
元(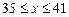 ),根据市场调查,日销售量与
),根据市场调查,日销售量与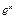 (
(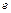 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.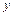 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价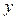 最大,并求
最大,并求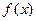 是定义在
是定义在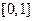 上的函数,若存在
上的函数,若存在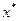
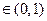 ,使得
,使得 上单调递增,在
上单调递增,在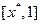 上单调递减,则称
上单调递减,则称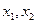
 ,若
,若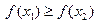 ,则
,则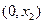 为含峰区间;若
为含峰区间;若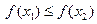 ,则
,则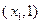 为含峰区间;
为含峰区间; ,证明:存在
,证明:存在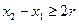 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于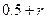 ;
; 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)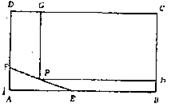
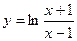 ,
,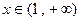 的反函数是【 】.
的反函数是【 】.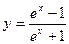
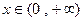
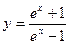
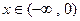
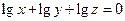 ,则
,则 .
.