题目内容
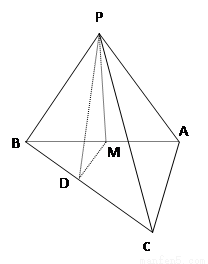
如图，△ABC中，AB=9，AC=6，点E在AB上且AE=3，点F在AC上，连接EF，若△AEF与△ABC相似，则AF=分析：根据题意，要使△AEF与△ABC相似，由于本题没有说明对应关系，故采用分类讨论法．有两种可能：当△AEF∽△ABC时；当△AEF∽△ACB时．最后利用相似三角形的对应边成比例即可求得线段AF的长即可．
解答：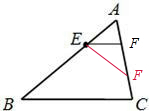
解：当△AEF∽△ABC时，则
=
，
=
，AF=2；
当△AEF∽△ACB时，则
=
，
=
，AF=4.5．
故答案为：2或4.5．
解：当△AEF∽△ABC时，则 | AE |
| AF |
| AB |
| AC |
| 3 |
| AF |
| 9 |
| 6 |
当△AEF∽△ACB时，则
| AE |
| AF |
| AC |
| AB |
| 3 |
| AF |
| 6 |
| 9 |
故答案为：2或4.5．
点评：本题考查相似三角形的性质应用．利用相似三角形的性质时，要注意相似比的顺序．分类讨论时，要注意对应关系的变化，防止遗漏．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，△ABC中，∠A=90°，AB=4，AC=3，平面ABC外一点P在平面ABC内的射影是AB中点M，二面角P-AC-B的大小为45°．
如图在△ABC中，AB⊥AC，
