题目内容
(本题满分12分)如图,四棱锥 中,底面
中,底面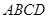 为矩形,
为矩形,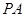 ⊥底面
⊥底面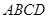 ,
,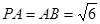 ,点
,点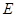 是棱
是棱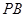 的中点.
的中点.
(Ⅰ)求点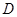 到平面
到平面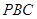 的距离;
的距离;
(Ⅱ) 若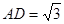 ,求二面角
,求二面角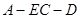 的平面角的余弦值 .
的平面角的余弦值 .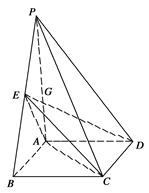
 中,底面
中,底面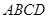 为矩形,
为矩形,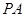 ⊥底面
⊥底面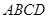 ,
,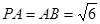 ,点
,点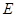 是棱
是棱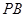 的中点.
的中点. (Ⅰ)求点
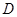 到平面
到平面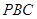 的距离;
的距离;(Ⅱ) 若
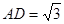 ,求二面角
,求二面角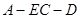 的平面角的余弦值 .
的平面角的余弦值 .
(Ⅰ)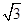 ;(Ⅱ)
;(Ⅱ)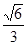
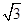 ;(Ⅱ)
;(Ⅱ)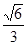
(I)可以利用体积法求解,根据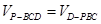 .也可利用向量法.
.也可利用向量法.
(II)可以考虑向量法,建系后,求出二面角两个面的法向量,然后求出法向量的夹角,再根据法向量的夹角与二面角相等或互补求解.
解:(Ⅰ)以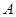 为坐标原点,射线
为坐标原点,射线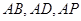 分别为
分别为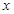 轴、
轴、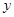 轴、
轴、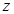 轴正半轴,建立空间直角坐标系
轴正半轴,建立空间直角坐标系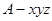 ,设
,设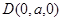 ,则
,则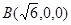 ,
, ,
,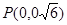 ,
, 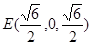 .因此
.因此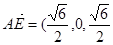 ),
),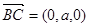 ,
,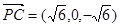 .
.
则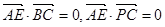 ,所以
,所以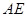 ⊥平面
⊥平面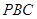 .又由
.又由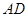 ∥
∥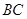 知
知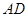 ∥平面
∥平面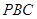 ,故点
,故点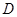 到平面
到平面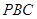 的距离为点
的距离为点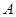 到平面
到平面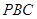 的距离,即为
的距离,即为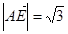 …(6分)
…(6分)
(Ⅱ)因为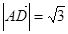 ,则
,则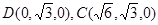 .设平面
.设平面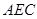 的法向量
的法向量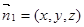 ,则由
,则由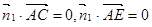 可解得:
可解得: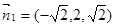 ,同理可解得
,同理可解得
平面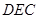 的法向量
的法向量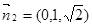 ,故
,故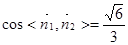
所以二面角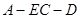 的平面角的余弦值为
的平面角的余弦值为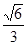 . ……(12分)
. ……(12分)
注:此题也可用传统法解答,可类似给分.
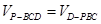 .也可利用向量法.
.也可利用向量法.(II)可以考虑向量法,建系后,求出二面角两个面的法向量,然后求出法向量的夹角,再根据法向量的夹角与二面角相等或互补求解.
解:(Ⅰ)以
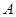 为坐标原点,射线
为坐标原点,射线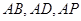 分别为
分别为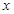 轴、
轴、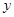 轴、
轴、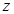 轴正半轴,建立空间直角坐标系
轴正半轴,建立空间直角坐标系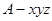 ,设
,设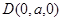 ,则
,则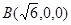 ,
, ,
,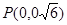 ,
, 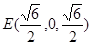 .因此
.因此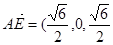 ),
),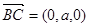 ,
,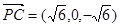 .
.则
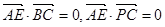 ,所以
,所以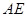 ⊥平面
⊥平面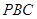 .又由
.又由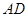 ∥
∥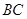 知
知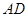 ∥平面
∥平面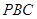 ,故点
,故点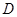 到平面
到平面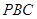 的距离为点
的距离为点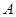 到平面
到平面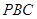 的距离,即为
的距离,即为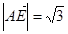 …(6分)
…(6分)(Ⅱ)因为
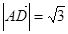 ,则
,则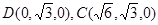 .设平面
.设平面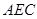 的法向量
的法向量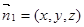 ,则由
,则由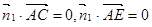 可解得:
可解得: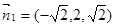 ,同理可解得
,同理可解得平面
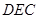 的法向量
的法向量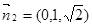 ,故
,故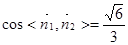
所以二面角
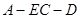 的平面角的余弦值为
的平面角的余弦值为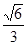 . ……(12分)
. ……(12分)注:此题也可用传统法解答,可类似给分.

练习册系列答案
相关题目
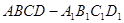 ,下列说法正确的有: ____________.
,下列说法正确的有: ____________.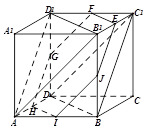
 点在线段
点在线段 上运动,棱锥
上运动,棱锥 体积不变;
体积不变;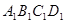 平行;
平行;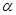 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形;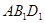 与平面
与平面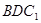 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。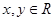 ,则
,则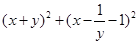 的最小值为( )
的最小值为( )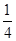
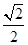
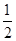

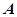 的坐标是(1,1,0), 点
的坐标是(1,1,0), 点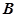 的坐标是(0,1,2), 则
的坐标是(0,1,2), 则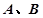 两点间距离为 。
两点间距离为 。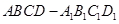 中,
中,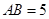 ,
,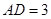 ,
,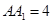 ,
,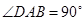 ,
,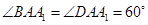 ,
,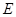 是
是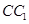 的中点,设
的中点,设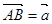 ,
,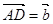 ,
,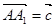 .
.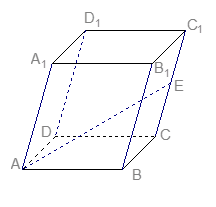
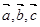 表示
表示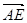 ;
;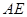 的长.
的长. 被圆
被圆 截得的弦长为
截得的弦长为 
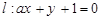 的距离相等,则a的值( )
的距离相等,则a的值( )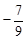
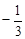
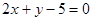 的距离等于
的距离等于