题目内容
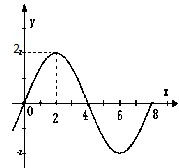 已知函数f(x)=Asin(ωx+?),(A>0,ω>0,0≤?≤π)的部分图象如图所示,记
已知函数f(x)=Asin(ωx+?),(A>0,ω>0,0≤?≤π)的部分图象如图所示,记| n |
 |
| i=1 |
| 27 |
 |
| i=1 |
2+2
| 2 |
2+2
.| 2 |
分析:先求出函数f(x)=2sin(
x),求出f(1)、f(2)、f(3)、…f(8 )的值,根据函数的周期性求出
f(i)的值.
| π |
| 4 |
| 27 |
 |
| i=1 |
解答:解:由函数f(x)的图象可得,此函数的周期等于8,A=2,∴
=8,ω=
.
把点(0,0)代入函数f(x)的解析式可得∅=0.
故函数f(x)=2sin(
x).f(1)=
,f(2)=2,f(3)=
,f(4)=0,
f(5)=-
,f(6)=-2,f(7)=-
,f(8)=0.
故 f(1)+f(2)+f(3)+…+f(8)=0.
∴
f(i)=
f(i)+f(25)+f(26)+f(27)=0+f(1)+f(2)+f(3)=2+2
.
故答案为:2+2
.
| 2π |
| ω |
| π |
| 4 |
把点(0,0)代入函数f(x)的解析式可得∅=0.
故函数f(x)=2sin(
| π |
| 4 |
| 2 |
| 2 |
f(5)=-
| 2 |
| 2 |
故 f(1)+f(2)+f(3)+…+f(8)=0.
∴
| 27 |
 |
| i=1 |
| 24 |
 |
| i=1 |
| 2 |
故答案为:2+2
| 2 |
点评:本题主要考查函数f(x)=Asin(ωx+?)的周期性以及根据图象求解析式,求出函数f(x)=2sin(
x),是解题的关键.
| π |
| 4 |

练习册系列答案
相关题目