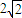题目内容
已知各项为正的等比数列的前5项之和为3,前15项之和为39,则该数列的前10项之和为( )
分析:设该数列的前n项和为Sn,由S5,S10-S5,S15-S10仍成等比数列可得关于S10的方程,解之可得.
解答:解:设该数列的前n项和为Sn,
由题意可得S5=3,S15=39,
由等比数列的性质可得S5,S10-S5,S15-S10仍成等比数列,
即(S10-3)2=3(39-S10),解之可得S10=12,或S10=-9,
因为数列的各项均为正数,故应舍去S10=-9,
故选C
由题意可得S5=3,S15=39,
由等比数列的性质可得S5,S10-S5,S15-S10仍成等比数列,
即(S10-3)2=3(39-S10),解之可得S10=12,或S10=-9,
因为数列的各项均为正数,故应舍去S10=-9,
故选C
点评:本题考查等比数列的求和公式和性质,得出S5,S10-S5,S15-S10仍成等比数列是解决问题的关键,属中档题.

练习册系列答案
相关题目
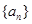 中,
中,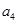 与
与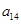 的等比中项为
的等比中项为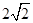 ,则
,则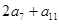 的最小值为 .
的最小值为 .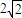 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )