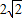题目内容
已知各项为正的等比数列{an}中,a4与a14的等比中项为2
,则2a7+a11的最小值为( )
| 2 |
分析:由各项为正的等比数列{an}中,a4与a14的等比中项为2
,知a4•a14=(2
)2=8,故a7•a11=8,利用均值不等式能够求出2a7+a11的最小值.
| 2 |
| 2 |
解答:解:∵各项为正的等比数列{an}中,a4与a14的等比中项为2
,
∴a4•a14=(2
)2=8,
∴a7•a11=8,
∵a7>0,a11>0,
∴2a7+a11≥2
=2
=8.
故选B.
| 2 |
∴a4•a14=(2
| 2 |
∴a7•a11=8,
∵a7>0,a11>0,
∴2a7+a11≥2
| 2a7•a11 |
| 2×8 |
故选B.
点评:本题考查等比数列的通项公式的应用,是中档题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
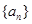 中,
中,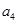 与
与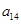 的等比中项为
的等比中项为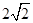 ,则
,则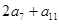 的最小值为 .
的最小值为 .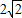 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )