题目内容
(本小题满分12分)已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(Ⅰ)若用数组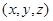 中的
中的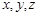 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组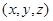 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由。
【答案】
(1)8;(2)猜4或5获奖的可能性最大.
【解析】第一问中,先分析所有的情况为共有8种,
第二问,由于事件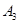 包含1个基本事件,事件
包含1个基本事件,事件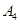 包含3个基本事件,事件
包含3个基本事件,事件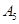 包含3个基本事件,事件
包含3个基本事件,事件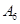 包含1个基本事件,然后利用古典概型的概率计算公式得到,比较大小即可。
包含1个基本事件,然后利用古典概型的概率计算公式得到,比较大小即可。
解:(Ⅰ)数组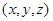 的所有情形为:(1,1,1),(1,1,2),(1,2,1),
的所有情形为:(1,1,1),(1,1,2),(1,2,1),
(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种.
答:一共有8种. ………………………5分
注:列出5、6、7种情形,得2分;列出所有情形,得4分;写出所有情形共8种,得1分.
(Ⅱ)记“所摸出的三个球号码之和为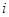 ”为事件
”为事件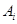 (
(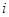 =3,4,5,6), ………6分
=3,4,5,6), ………6分
易知,事件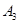 包含1个基本事件,事件
包含1个基本事件,事件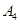 包含3个基本事件,事件
包含3个基本事件,事件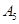 包含3个基本事件,事件
包含3个基本事件,事件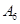 包含1个基本事件,所以,
包含1个基本事件,所以,
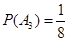 ,
,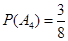 ,
,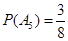 ,
,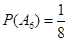 . ……………………10分
. ……………………10分
故所摸出的两球号码之和为4、为5的概率相等且最大.
答:猜4或5获奖的可能性最大. ……………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目