题目内容
在Z轴上有一点M,使得M到点A(1,0,2)与点B(1,-3,1)的距离相等,则M的坐标为______.
设z轴上满足条件的点为M(0,0,z),
∵点M到点A(1,0,2)与点B(1,-3,1)的距离相等,
∴|AM|=|BM|,即
=
,
解之得z=-3,得M(0,0,-3).
故答案为:(0,0,-3).
∵点M到点A(1,0,2)与点B(1,-3,1)的距离相等,
∴|AM|=|BM|,即
| (1-0)2+(0-0)2+(2-z)2 |
| (1-0)2+(-3-0)2+(1-z)2 |
解之得z=-3,得M(0,0,-3).
故答案为:(0,0,-3).

练习册系列答案
相关题目
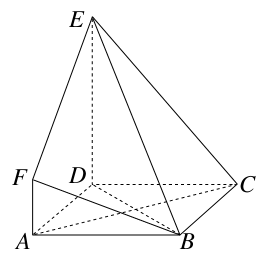
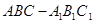 中,
中,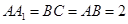 ,
,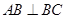 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。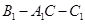 的大小。
的大小。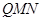 ⊥平面
⊥平面 ,
, 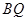 的长度。
的长度。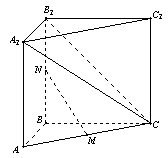
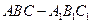 的各棱长都2,E,F分别是
的各棱长都2,E,F分别是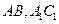 的中点,则EF的长是
的中点,则EF的长是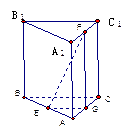



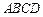 是边长为
是边长为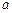 的正方形,
的正方形,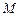 、
、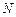 分别是边
分别是边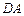 、
、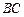 上的点(M不与A、D重合),且
上的点(M不与A、D重合),且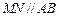 ,
,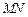 交
交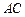 于点
于点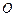 ,沿
,沿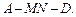
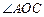 的大小是否发生变化?试说明理由;
的大小是否发生变化?试说明理由;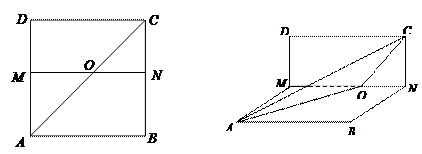 (2)当
(2)当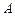 、
、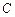 两点间的距离最小?并求出这个最小值.
两点间的距离最小?并求出这个最小值.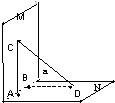
 中,点
中,点 ,
, 的中点为
的中点为 ,重心为
,重心为 ,则边
,则边 的长为( )
的长为( )


