题目内容
数列{an}满足a1=2,an+1=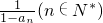 ,则{an}的前2012项的和为.________.
,则{an}的前2012项的和为.________.
1006
分析:先确定数列{an}是以3为周期的周期数列,再求{an}的前2012项的和.
解答:∵数列{an}满足a1=2,an+1=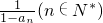
∴a2=-1,a3= ,a4=2
,a4=2
∴数列{an}是以3为周期的周期数列,且前3项的和为
∴{an}的前2012项的和为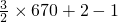 =1006
=1006
故答案为1006
点评:本题考查数列递推式,考查正确数列,考查数列的求和,确定数列{an}是以3为周期的周期数列是关键.
分析:先确定数列{an}是以3为周期的周期数列,再求{an}的前2012项的和.
解答:∵数列{an}满足a1=2,an+1=
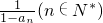
∴a2=-1,a3=
 ,a4=2
,a4=2∴数列{an}是以3为周期的周期数列,且前3项的和为

∴{an}的前2012项的和为
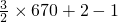 =1006
=1006故答案为1006
点评:本题考查数列递推式,考查正确数列,考查数列的求和,确定数列{an}是以3为周期的周期数列是关键.

练习册系列答案
相关题目