题目内容
下列命题:①“
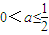 ”是“存在n∈N*,使得
”是“存在n∈N*,使得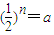 成立”的充分条件;
成立”的充分条件;②“a>0”是“存在n∈N*,使得
 成立”的必要条件;
成立”的必要条件;③“
 ”是“不等式
”是“不等式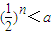 对一切n∈N*恒成立”的充要条件.
对一切n∈N*恒成立”的充要条件.其中所以真命题的序号是( )
A.③
B.②③
C.①②
D.①③
【答案】分析:选项①“ ”应是“存在n∈N*,使得
”应是“存在n∈N*,使得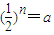 成立”的充要条件;选项②当存在n∈N*,使得
成立”的充要条件;选项②当存在n∈N*,使得 成立时,a只需大于
成立时,a只需大于 当n∈N*,时的最小取值即可,可得a>0;选项③由充要条件的证明方法可得.
当n∈N*,时的最小取值即可,可得a>0;选项③由充要条件的证明方法可得.
解答:解:选项①当 时,不一定存在n∈N*,使得
时,不一定存在n∈N*,使得 成立,
成立,
比如取a= ,则不存在自然数n,使
,则不存在自然数n,使 ,故前者是后者的非充分充分条件,
,故前者是后者的非充分充分条件,
但存在n∈N*,使得 成立时,a即为
成立时,a即为 当n∈N*,时的取值范围,即
当n∈N*,时的取值范围,即 ,
,
故“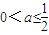 ”应是“存在n∈N*,使得
”应是“存在n∈N*,使得 成立”的必要非充分条件,故①错误;
成立”的必要非充分条件,故①错误;
选项②当存在n∈N*,使得 成立时,a只需大于
成立时,a只需大于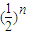 当n∈N*,时的最小取值即可,
当n∈N*,时的最小取值即可,
故可得a>0,故“a>0”是“存在n∈N*,使得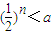 成立”的必要条件,故②正确;
成立”的必要条件,故②正确;
选项③由①知,当n∈N*时 的取值范围为
的取值范围为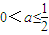 ,
,
故当 时,必有“不等式
时,必有“不等式 对一切n∈N*恒成立”,
对一切n∈N*恒成立”,
而要使不等式 对一切n∈N*恒成立”,只需a大于
对一切n∈N*恒成立”,只需a大于 的最大值即可,即a
的最大值即可,即a
故“ ”是“不等式
”是“不等式 对一切n∈N*恒成立”的充要条件.
对一切n∈N*恒成立”的充要条件.
故选B
点评:本题考查命题真假的判断与应用,涉及指数函数和恒成立问题,属基础题.
 ”应是“存在n∈N*,使得
”应是“存在n∈N*,使得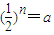 成立”的充要条件;选项②当存在n∈N*,使得
成立”的充要条件;选项②当存在n∈N*,使得 成立时,a只需大于
成立时,a只需大于 当n∈N*,时的最小取值即可,可得a>0;选项③由充要条件的证明方法可得.
当n∈N*,时的最小取值即可,可得a>0;选项③由充要条件的证明方法可得.解答:解:选项①当
 时,不一定存在n∈N*,使得
时,不一定存在n∈N*,使得 成立,
成立,比如取a=
 ,则不存在自然数n,使
,则不存在自然数n,使 ,故前者是后者的非充分充分条件,
,故前者是后者的非充分充分条件,但存在n∈N*,使得
 成立时,a即为
成立时,a即为 当n∈N*,时的取值范围,即
当n∈N*,时的取值范围,即 ,
,故“
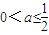 ”应是“存在n∈N*,使得
”应是“存在n∈N*,使得 成立”的必要非充分条件,故①错误;
成立”的必要非充分条件,故①错误;选项②当存在n∈N*,使得
 成立时,a只需大于
成立时,a只需大于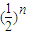 当n∈N*,时的最小取值即可,
当n∈N*,时的最小取值即可,故可得a>0,故“a>0”是“存在n∈N*,使得
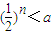 成立”的必要条件,故②正确;
成立”的必要条件,故②正确;选项③由①知,当n∈N*时
 的取值范围为
的取值范围为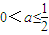 ,
,故当
 时,必有“不等式
时,必有“不等式 对一切n∈N*恒成立”,
对一切n∈N*恒成立”,而要使不等式
 对一切n∈N*恒成立”,只需a大于
对一切n∈N*恒成立”,只需a大于 的最大值即可,即a
的最大值即可,即a
故“
 ”是“不等式
”是“不等式 对一切n∈N*恒成立”的充要条件.
对一切n∈N*恒成立”的充要条件.故选B
点评:本题考查命题真假的判断与应用,涉及指数函数和恒成立问题,属基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
在空间中,下列命题正确的是( )
| A、如果一个角的两边和另一角的两边分别平行,那么这两个角相等 | ||
B、两条异面直线所成的有的范围是[0,
| ||
| C、如果两个平行平面同时与第三个平面相交,那么它们的交线平行 | ||
| D、如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行 |
下列命题错误的是( )
| A、锐角都是第一象限角 | B、顺时针旋转所形成的角为负角 | C、始边与终边重合的角一定是零角 | D、终边相同的角的三角函数值一定相等 |