题目内容
13.函数f(x)=$\frac{1}{2}$x2+x-2lnx+a在区间(1,2)上恰有一个零点,则实数a的取值范围为2ln2-4<a<-$\frac{3}{2}$.分析 由题设条件利用导数性质推导出f(x)在(1,2)上递增,要使f(x)在(1,2)上恰有一个零点,需要f(1)<0,f(2)>0,由此能求出实数a取值范围.
解答 解:∵f′(x)=x+1-$\frac{2}{x}$=$\frac{(x+2)(x-1)}{x}$,x∈(1,2),
∴f′(x)>0,f(x)在(1,2)递增,
若函数f(x)在(1,2)只有1个零点,
则$\left\{\begin{array}{l}{f(1)=\frac{3}{2}+a<0}\\{f(2)=4-2ln2+a>0}\end{array}\right.$,解得:2ln2-4<a<-$\frac{3}{2}$,
故答案为:$2ln2-4<a<-\frac{3}{2}$.
点评 本题考查利用导数研究函数的极值的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
1.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≥2\\ 2x+y≥2\\ x≥0,y≥0\end{array}\right.$则z=x+5y的最小值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
2.设点M(1,y0),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则y0的取值范围是( )
| A. | [-1,1] | B. | [-$\frac{1}{2},\frac{1}{2}$] | C. | [-$\sqrt{2},\sqrt{2}$] | D. | [-$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$] |
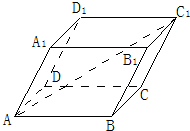 已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.
已知平行六面体,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,求|$\overrightarrow{A{C}_{1}}$|.