题目内容
分别求下列函数的值域:(1)y=
| 2x+1 |
| x-3 |
(2)y=-x2+2x(x∈[0,3]);
(3)y=x+
| 1-x2 |
(4)y=
| 1-2x |
| 1+2x |
分析:(1)用分离变量法将原函数变形,再根据分母不为零,求函数的值域;
(2)用配方法将原函数变形,再根据开口方向和对称轴的大小,求出在区间上的最值,在表示出值域;
(3)先求函数定义域[-1,1],故设x=cosθ(θ∈[0,π]),代入原函数利用两角的和差公式进行化简,再利用正弦函数的曲线求出最值,即求出值域;
(4)用分离变量法将原函数变形,利用2x>0求原函数的值域.
(2)用配方法将原函数变形,再根据开口方向和对称轴的大小,求出在区间上的最值,在表示出值域;
(3)先求函数定义域[-1,1],故设x=cosθ(θ∈[0,π]),代入原函数利用两角的和差公式进行化简,再利用正弦函数的曲线求出最值,即求出值域;
(4)用分离变量法将原函数变形,利用2x>0求原函数的值域.
解答:解:(1)用分离变量法将原函数变形为:y=
=2+
.
∵x≠3,∴
≠0.
∴y≠2,即函数值域为{y|y∈R且y≠2}.
(2)用配方法将原函数变形为:y=-(x-1)2+1,根据二次函数的性质,
在区间[0,3]上,当x=1时,函数取最大值1,当x=3时,函数取最小值是-3,
则原函数的值域是[-3,1].
(3)由1-x2≥0,得-1≤x≤1,设x=cosθ(θ∈[0,π]),
则y=sinθ+cosθ=
sin(θ+
),
由正弦函数曲线易知,当θ=
时,y取最大值为
,当θ=π时,y取最小值为-1,
∴原函数的值域是[-1,
].
(4)分离常数法将原函数变形为:
y=
=
=-1+
∵1+2x>1,∴0<
<2,
∴-1<-1+
<1,
∴所求值域为(-1,1)
| 2x-6+7 |
| x-3 |
| 7 |
| x-3 |
∵x≠3,∴
| 7 |
| x-3 |
∴y≠2,即函数值域为{y|y∈R且y≠2}.
(2)用配方法将原函数变形为:y=-(x-1)2+1,根据二次函数的性质,
在区间[0,3]上,当x=1时,函数取最大值1,当x=3时,函数取最小值是-3,
则原函数的值域是[-3,1].
(3)由1-x2≥0,得-1≤x≤1,设x=cosθ(θ∈[0,π]),
则y=sinθ+cosθ=
| 2 |
| π |
| 4 |
由正弦函数曲线易知,当θ=
| π |
| 4 |
| 2 |
∴原函数的值域是[-1,
| 2 |
(4)分离常数法将原函数变形为:
y=
| 1-2x |
| 1+2x |
| -2x-1+2 |
| 1+2x |
| 2 |
| 1+2x |
∵1+2x>1,∴0<
| 2 |
| 1+2x |
∴-1<-1+
| 2 |
| 1+2x |
∴所求值域为(-1,1)
点评:本题考查了求函数值域的方法,即分离常数法,配方法和换元法等,注意每种方法适用的类型.

练习册系列答案
相关题目
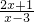 ;
; ;
; .
.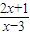 ;
;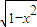 ;
;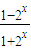 .
.