题目内容
(1)求值sin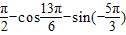
(2)已知
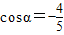 ,
,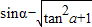 的值.
的值.
【答案】分析:(1)本题是一个利用诱导公式进行恒等变形化简,可先由公式化简,再代入特殊角的三角函数值计算出结果;
(2)本题是利用同角三角函数基本关系求值的题,由题意,可先求出角的余弦,再代入求值.
解答:(1)解:原式=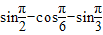 =1-
=1- -
-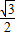 =
=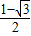
(2)解:由 ,故sinα=±
,故sinα=±
∴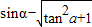 =
=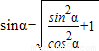 =
=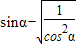 =
=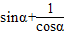 =±
=± -
-
即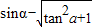 的值 为-
的值 为-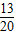 或-
或-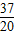
点评:本题考查同角三角函数关系及诱导公式化简求值,解题的关键是熟练掌握诱导公式及同角三角函数的关系,本题的难点是注意到角的正弦的符号,其有两种可能,这也是本题的易错点,解题时要考虑全面
(2)本题是利用同角三角函数基本关系求值的题,由题意,可先求出角的余弦,再代入求值.
解答:(1)解:原式=
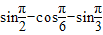 =1-
=1- -
-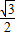 =
=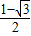
(2)解:由
 ,故sinα=±
,故sinα=±
∴
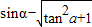 =
=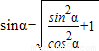 =
=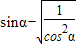 =
=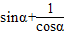 =±
=± -
-
即
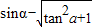 的值 为-
的值 为-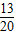 或-
或-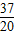
点评:本题考查同角三角函数关系及诱导公式化简求值,解题的关键是熟练掌握诱导公式及同角三角函数的关系,本题的难点是注意到角的正弦的符号,其有两种可能,这也是本题的易错点,解题时要考虑全面

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数
sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数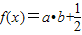 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为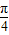 .
.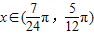 时,
时,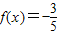 ,求cos4x的值;
,求cos4x的值;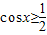 ,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.
,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.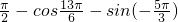
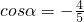 ,
,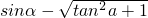 的值.
的值.