题目内容
求由直线y=x-2和曲线y=-x2所围成的图形的面积．
解：联立
，得x1=-2，x2=1．
所以，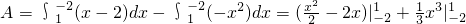
=
，
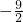故所求面积
．
分析：先求出直线y=x-2和曲线y=-x2的交点坐标，然后再根据定积分求图形面积．
点评：本题考查直线与圆锥曲线的综合问题，解题时要认真审题，仔细解答．
，得x1=-2，x2=1．所以，
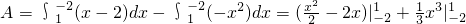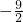=，故所求面积
．分析：先求出直线y=x-2和曲线y=-x2的交点坐标，然后再根据定积分求图形面积．
点评：本题考查直线与圆锥曲线的综合问题，解题时要认真审题，仔细解答．
练习册系列答案
同步练习强化拓展系列答案
相关题目