题目内容
已知圆C的圆心在直线 上,并且与直线
上,并且与直线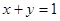 相切于点A(2,-1).
相切于点A(2,-1).
(Ⅰ)求圆C的方程;
(Ⅱ)从圆C外一点M引圆C的切线MN,N为切点,且MN=MO(O为坐标原点),求MN的最小值.
【答案】
(1)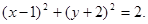 ;(2)MN的最小值为
;(2)MN的最小值为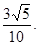 此时点M的坐标为
此时点M的坐标为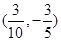 .
.
【解析】本试题主要是考查了直线与圆的方程,以及圆的切线方程的综合知识的运用。第一问中求解圆的方程,确定圆心和半径即可。第二问中,;利用设坐标,表示MN=MO,然后化简得到MN为一个元的二次函数形式,借助于二次函数的性质求解其最值的数学思想的运用。
解:(1)与直线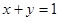 相切于点A(2,-1)的圆的圆心在经过点A且与直线
相切于点A(2,-1)的圆的圆心在经过点A且与直线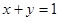 垂直的直线上,该直线的方程是
垂直的直线上,该直线的方程是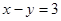 .
…………2分
.
…………2分
又所求圆的圆心在直线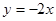 上,解方程组
上,解方程组
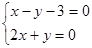
得x=1,y=-2.
所以圆心C的坐标是(1,-2). …………4分
因为|AC|=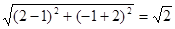 ,
…………5分
,
…………5分
所以所求圆的方程为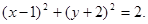 …………6分
…………6分
(2)设M(x,y),则MO=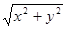 ,MN=
,MN=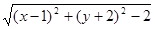 ,
,
由MN=MO,得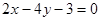 ,
…………8分
,
…………8分
MN=MO=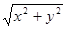 =
=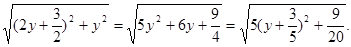
…………11分
当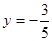 时,MN=
时,MN=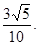 因此,MN的最小值为
因此,MN的最小值为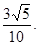 此时点M的坐标为
此时点M的坐标为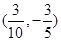 .
.
…………13分

练习册系列答案
相关题目