题目内容
函数 在区间
在区间 内的零点个数是( )
内的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:因为 ,所以函数
,所以函数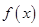 在
在 内有零点,又因为函数
内有零点,又因为函数 在区间
在区间 内单调递增,所以函数
内单调递增,所以函数 在区间
在区间 内由一个零点。
内由一个零点。
考点:零点存在性定理。
点评:零点存在性定理只能判断函数是否存在零点,但不能判断零点的个数。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义域为 的函数
的函数
 有四个单调区间,则实数
有四个单调区间,则实数 满足( )
满足( )
A. | B. | C. | D. |
函数f(x)= cos2x在区间[-3,3]上的零点的个数为( )
cos2x在区间[-3,3]上的零点的个数为( )
| A.3 | B.4 | C.5 | D.6 |
定义在R上的偶函数 满足:对任意的
满足:对任意的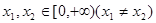 ,有
,有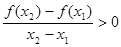 ,则( )
,则( )
A.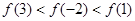 | B.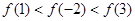 |
C.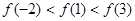 | D.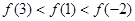 |
设偶函数 在
在 上是增函数,则
上是增函数,则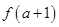 与
与 的
的
大小关系是( )
A. | B. |
C. | D.不能确定 |
下列函数中是偶函数且在 上单调递增的是 ( )
上单调递增的是 ( )
A. | B. | C. | D. |
函数 的定义域是
的定义域是
A.( ) ) | B.( | C. | D. ) ) |
 的图像大致是
的图像大致是
 的图像大致为 ( )
的图像大致为 ( )