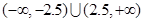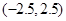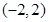题目内容
定义在R上的偶函数 满足:对任意的
满足:对任意的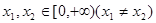 ,有
,有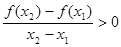 ,则( )
,则( )
A.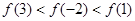 | B.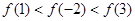 |
C.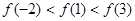 | D.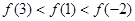 |
B
解析试题分析:因为对任意的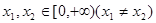 ,有
,有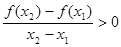 ,即
,即 ,所以函数
,所以函数 在
在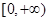 上单调递增。所以
上单调递增。所以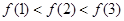 ,又因为f(2)=f(-2),所以
,又因为f(2)=f(-2),所以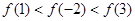 。
。
考点:函数的单调性和奇偶性的综合应用。
点评:灵活掌握函数单调性的定义:①若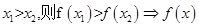 在D内单调递增;②若函数f(x)的定义域为D,对任意
在D内单调递增;②若函数f(x)的定义域为D,对任意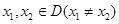 ,
,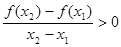
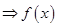 在D内单调递增;③若函数f(x)的定义域为D,对任意
在D内单调递增;③若函数f(x)的定义域为D,对任意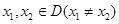 ,
,
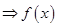 在D内单调递增.
在D内单调递增.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 零点的个数为( )
零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
定义域为R的函数 ,若关于
,若关于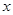 的方程
的方程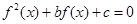 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 ( )
( )
| A.4 | B.10 | C.12 | D.16 |
函数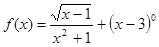 的定义域为( )
的定义域为( )
A.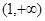 | B. | C.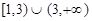 | D.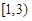 |
函数 在区间
在区间 内的零点个数是( )
内的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知函数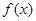 的定义域为
的定义域为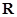 ,满足
,满足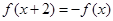 ,当
,当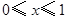 时,
时,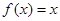 ,则
,则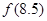 等( )
等( )
A.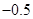 | B.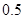 | C.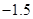 | D.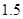 |
设 是函数
是函数 的反函数,若
的反函数,若 ,则
,则 的最小值是( )
的最小值是( )
| A.1 | B.2 | C. | D.4 |
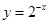 的图象大致是
的图象大致是
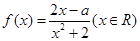 在区间
在区间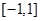 上是增函数,实数a组成几何A,设关于x的方程
上是增函数,实数a组成几何A,设关于x的方程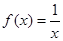 的两个非零实根
的两个非零实根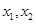 ,实数m使得不等式
,实数m使得不等式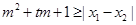 使得对任意
使得对任意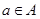 及
及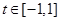 恒成立,则m的解集是( )
恒成立,则m的解集是( )