题目内容
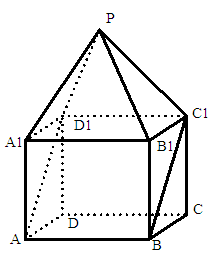
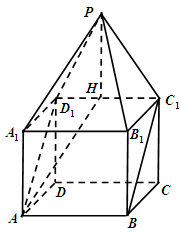
如图,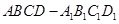 是棱长为1的正方体,四棱锥
是棱长为1的正方体,四棱锥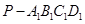 中,
中,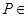 平面
平面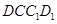 ,
,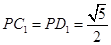 。
。
(Ⅰ)求证: 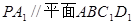
(Ⅱ)求直线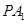 与平面
与平面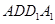 所成角的正切值。
所成角的正切值。
(Ⅰ) 先证明四边形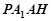 为平行四边形,∴
为平行四边形,∴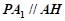 ,再利用线面平行的性质定理证明即可; (Ⅱ)
,再利用线面平行的性质定理证明即可; (Ⅱ) 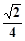
解析试题分析:(Ⅰ)取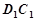 的中点
的中点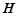 ,连结
,连结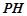 ,
,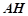 .
.
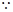
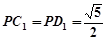 ,
,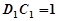 ,
, 平面
平面 ,
,
∴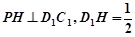 ,
,
∴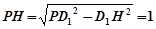 , ……1分
, ……1分
∴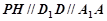 ,
, 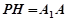 ,
,
∴四边形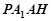 为平行四边形,
为平行四边形,
∴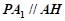 , ……3分
, ……3分
又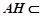 平面
平面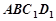 ,
, 平面
平面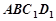 ,∴
,∴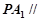 平面
平面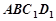 . ……5分
. ……5分
(Ⅱ)∵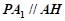 ,
,
∴直线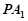 与平面
与平面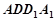 所成角等于直线
所成角等于直线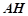 与平面
与平面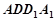 所成角.
所成角.
正方体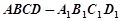 中,显然
中,显然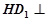 平面
平面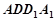 ,
,
∴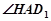 就是直线
就是直线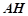 与平面
与平面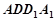 所成角. ……7分
所成角. ……7分
在 中,
中,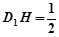 ,
,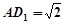 ,
,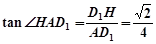 ,
,
∴直线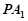 与平面
与平面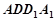 所成角的正切值为
所成角的正切值为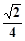 . ……10分
. ……10分
考点:本小题主要考查线面平行的证明,线面角的求解.
点评:要解决立体几何问题,要发挥空间想象能力,紧扣相应的判定定理和性质定理,定理中要求的条件要一一列举出来,求相应角时,要注意角的范围.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
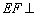 平面AEB,
平面AEB, ,
, ,
,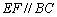 ,
,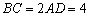 ,
,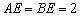 ,
, ,G是BC的中点.
,G是BC的中点.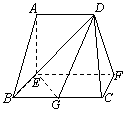
 ;
; 的大小.
的大小. 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱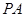 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点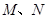 分别是
分别是 的中点.求
的中点.求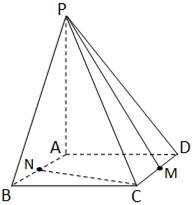
 与
与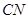 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);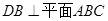 ,
,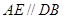 ,
,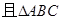 是边长为2的等边三角形,
是边长为2的等边三角形,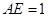 ,CD与平面ABDE所成角的正弦值为
,CD与平面ABDE所成角的正弦值为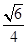 .
.
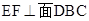 ,若存在,求线段DF的长度,若不存在,说明理由;
,若存在,求线段DF的长度,若不存在,说明理由;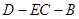 的平面角的余弦值.
的平面角的余弦值. ABC=60
ABC=60 ,EC
,EC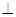 面ABCD,FA
面ABCD,FA
 BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
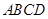 所在平面与平面四边形
所在平面与平面四边形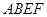 所在平面互相垂直,△
所在平面互相垂直,△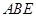 是等腰直角三角形,
是等腰直角三角形,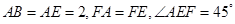
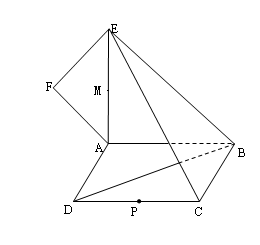
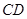 的中点为
的中点为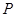 ,线段
,线段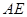 的中点为
的中点为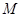 ,求证:
,求证: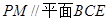 ;
;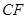 与平面
与平面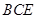 所成角的正切值.
所成角的正切值. ,VA =" 6."
,VA =" 6." 