题目内容
若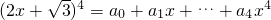 ,则(a0+a2+a4)2-(a1+a3)2的值为________.
,则(a0+a2+a4)2-(a1+a3)2的值为________.
1
分析:根据所给的等式,给变量赋值,当x为-1时,得到一个等式,当x为1时,得到另一个等式,而(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4),代入即可求得结果.
解答:∵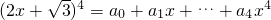 ,
,
当x=-1时,(-2 )4=a0-a1+a2-a3+a4①
)4=a0-a1+a2-a3+a4①
当x=1时,(2 )4=a0+a1+a2+a3+a4②
)4=a0+a1+a2+a3+a4②
而(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)
=(2 )4(-2
)4(-2 )4=1
)4=1
∴(a0+a2+a4)2-(a1+a3)2=1,
故答案为1.
点评:此题是个基础题.本题考查二项式定理的性质,考查的是给变量赋值的问题,结合要求的结果,观察所赋得值,当变量为-1时,当变量为0时,两者结合可以得到结果.
分析:根据所给的等式,给变量赋值,当x为-1时,得到一个等式,当x为1时,得到另一个等式,而(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4),代入即可求得结果.
解答:∵
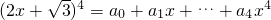 ,
,当x=-1时,(-2
 )4=a0-a1+a2-a3+a4①
)4=a0-a1+a2-a3+a4①当x=1时,(2
 )4=a0+a1+a2+a3+a4②
)4=a0+a1+a2+a3+a4②而(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)
=(2
 )4(-2
)4(-2 )4=1
)4=1∴(a0+a2+a4)2-(a1+a3)2=1,
故答案为1.
点评:此题是个基础题.本题考查二项式定理的性质,考查的是给变量赋值的问题,结合要求的结果,观察所赋得值,当变量为-1时,当变量为0时,两者结合可以得到结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
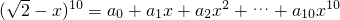 ,则(a0+a2+…+a10)2-(a1+a3+…+a9)2的值为
,则(a0+a2+…+a10)2-(a1+a3+…+a9)2的值为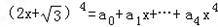 ,则(a0+a2+a4)2﹣(a1+a3)2的值为( ).
,则(a0+a2+a4)2﹣(a1+a3)2的值为( ).