题目内容
若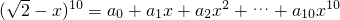
，则（a0+a2+…+a10）2-（a1+a3+…+a9）2的值为
- A.0
- B.2
- C.-1
- D.1
D
分析：因为题目已知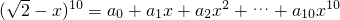，则求（a0+a2+…+a10）2-（a1+a3+…+a9）2
故可设设f（x）=（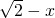
）10，又式子（a0+a2+…+a10）2-（a1+a3+…+a9）2可以根据平方差化简成两个式子的乘积，再根据二项式系数的性质可得它们等于f（1）f（-1），解出即可得到答案．
解答：设f（x）=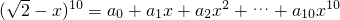
则（a0+a2+…+a10）2-（a1+a3+…+a9）2=（a0+a1+…+a10）（a0-a1+a2-…-a9+a10）=f（1）f（-1）
=（
）10（
）10=1．
故选D．
点评：此题主要考查二项式系数的性质的应用问题，其中判断出（a0+a1+…+a10）（a0-a1+a2-…-a9+a10）=f（1）f（-1）是题目关键，有一定的技巧性，属于中档题目．
分析：因为题目已知
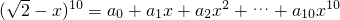，则求（a0+a2+…+a10）2-（a1+a3+…+a9）2故可设设f（x）=（
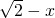）10，又式子（a0+a2+…+a10）2-（a1+a3+…+a9）2可以根据平方差化简成两个式子的乘积，再根据二项式系数的性质可得它们等于f（1）f（-1），解出即可得到答案．解答：设f（x）=
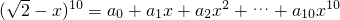
则（a0+a2+…+a10）2-（a1+a3+…+a9）2=（a0+a1+…+a10）（a0-a1+a2-…-a9+a10）=f（1）f（-1）
=（
）10（）10=1．故选D．
点评：此题主要考查二项式系数的性质的应用问题，其中判断出（a0+a1+…+a10）（a0-a1+a2-…-a9+a10）=f（1）f（-1）是题目关键，有一定的技巧性，属于中档题目．
练习册系列答案
相关题目
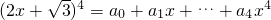，则（a0+a2+a4）2-（a1+a3）2的值为________．
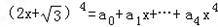，则（a0+a2+a4）2﹣（a1+a3）2的值为（ ）．